Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-22T21:58:02.171Z Has data issue: false hasContentIssue false
  • English
  • Français

The General Structure of G-Graded Contractions of Lie Algebras I. The Classification

Published online by Cambridge University Press:  20 November 2018

Evelyn Weimar-Woods
Evelyn Weimar-Woods*
Affiliation:
Fachbereich für Mathematik und Informatik, Freie Universität Berlin, Arnimallee 2-6, D-14195 Berlin, Germany e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give the general structure of complex (resp., real) 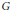$G$-graded contractions of Lie algebras where 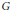$G$ is an arbitrary finite Abelian group. For this purpose, we introduce a number of concepts, such as pseudobasis, higher-order identities, and sign invariants. We characterize the equivalence classes of 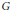$G$-graded contractions by showing that our set of invariants (support, higher-order identities, and sign invariants) is complete, which yields a classification.

Keywords

17B0517B70Lie algebrasgraded contractions
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 58 , Issue 6 , 01 December 2006 , pp. 1291 - 1340
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Couture, M., Patera, J., Sharp, R. T. and Winternitz, P., Graded contractions of sl(3, ℂ). J. Math. Phys. 32(1991), 2310–2318.Google Scholar
[2] Hussin, A., King, R. C., Leng, X. and Patera, J., Graded contractions of the affine Lie algebra , its representations and tensor products, and an application to the branching rule . J. Phys. A 27(1994), no. 12, 4125–4125.Google Scholar
[3] Inönü, E. and Wigner, E. P., On the contraction of groups and their representations. Proc. Nat. Acad. Sci. U.S.A. 39(1953), 510–524.Google Scholar
[4] de Montigny, M. and Patera, J., Discrete and continuous graded contractions of Lie algebras and superalgebras. J. Phys. A 24(1991) no. 3, 525–547.Google Scholar
[5] de Montigny, M., Patera, J. and Tolar, J., Graded contractions and kinematical groups of space-time. J. Math. Phys. 35(1994), no. 1, 405–425.Google Scholar
[6] Moody, R. V. and Patera, J., Discrete and continuous graded contractions of representations of Lie algebras. J. Phys. A 24(1991) no. 10, 2227–2257.Google Scholar
[7] Patera, J., Pogosyan, G. and Winternitz, P., Graded contractions of the Lie algebra. (2, 1), J. Phys. A 32(1999), 805–826.Google Scholar
[8] Rotman, J. J., The Theory of Groups. An Introduction. Allyn and Bacon, Boston, 1973.Google Scholar
[9] Saletan, E. J., Contractions of Lie groups. J. Math. Phys. 2(1961), 1–21.Google Scholar
[10] Segal, I. E., A class of operator algebras which are determined by groups. Duke Math. J. 18(1951), 221–265.Google Scholar
[11] Tolar, J. and Trávniček, P., Graded contractions and the conformal group of Minkowski space-time. J. Math. Phys. 36(1995), no. 8, 4489–4506.Google Scholar
[12] Tolar, J. and Trávniček, P., Graded contractions of symplectic Lie algebras in collective models, J. Math. Phys. 38(1997) no. 1, 501–523.Google Scholar
[13] Weimar-Woods, E., Contractions of Lie algebras. Generalized Inönü-Wigner contractions versus graded contractions. J. Math. Phys. 36(1995), no. 8, 4519–4548.Google Scholar
[14] Weimar-Woods, E., Contractions, generalized Inönü-Wigner contractions and deformations of finite-dimensional Lie algebras. Rev. Math. Phys. 12(2000), no. 11, 1505–1529.Google Scholar
[15] Weimar-Woods, E., The general structure of G-graded contractions of Lie algebras. II. The contracted Lie algebra. Rev. Math. Phys. 18(2006), no. 6, 655–711.Google Scholar