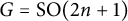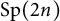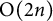1 Introduction
Let F be a non-Archimedean local field of residue characteristic q. Let G be the group of F-points of a connected, split reductive algebraic group defined over F; in particular, the group G contains a Borel subgroup. Let U be the unipotent radical of the Borel subgroup, and fix a nondegenerate (Whittaker) character
![]() $\psi : U \rightarrow {\mathbb C}^{\times }$
. The Gelfand–Graev representation of G is
$\psi : U \rightarrow {\mathbb C}^{\times }$
. The Gelfand–Graev representation of G is
![]() ${\mathrm {c-ind}}_U^G (\psi )$
, where
${\mathrm {c-ind}}_U^G (\psi )$
, where
![]() ${\mathrm {c-ind}}$
stands for induction with compact support. The goal of this paper is to give an explicit description of the Bernstein components of the Gelfand–Graev representation.
${\mathrm {c-ind}}$
stands for induction with compact support. The goal of this paper is to give an explicit description of the Bernstein components of the Gelfand–Graev representation.
Let us briefly describe what is known. Let K be a special maximal compact subgroup of G, and let I be an Iwahori subgroup contained in K. Let
![]() ${\mathcal H}$
be the Iwahori–Hecke algebra of I-biinvariant functions on G, and let
${\mathcal H}$
be the Iwahori–Hecke algebra of I-biinvariant functions on G, and let
![]() ${\mathcal H}_K$
be the subalgebra consisting of functions supported on K. Then
${\mathcal H}_K$
be the subalgebra consisting of functions supported on K. Then
![]() ${\mathcal H}_K$
is isomorphic to the group algebra of the Weyl group W of G, and thus it has a one-dimensional representation
${\mathcal H}_K$
is isomorphic to the group algebra of the Weyl group W of G, and thus it has a one-dimensional representation
![]() $\epsilon $
(the sign character). As an
$\epsilon $
(the sign character). As an
![]() ${\mathcal H}$
-module,
${\mathcal H}$
-module,
![]() $({\mathrm {c-ind}}^{G}_U \psi )^I$
is isomorphic to the projective
$({\mathrm {c-ind}}^{G}_U \psi )^I$
is isomorphic to the projective
![]() $\mathcal {H}$
-module [Reference Chan and Savin10]
$\mathcal {H}$
-module [Reference Chan and Savin10]
If
![]() $G=\mathrm {GL}_n$
, then a similar statement holds for all Bernstein components with appropriate Hecke algebras arising from Bushnell–Kutzko types [Reference Chan and Savin11]. We build on methods of that paper. We finish this paragraph by mentioning a recent article of Mishra and Pattanayak [Reference Mishra and Pattanayak20] that considers Bernstein components of
$G=\mathrm {GL}_n$
, then a similar statement holds for all Bernstein components with appropriate Hecke algebras arising from Bushnell–Kutzko types [Reference Chan and Savin11]. We build on methods of that paper. We finish this paragraph by mentioning a recent article of Mishra and Pattanayak [Reference Mishra and Pattanayak20] that considers Bernstein components of
![]() ${\mathrm {c-ind}}_U^G (\psi )$
corresponding to representations induced from the Borel subgroup. Their result is formulated in terms of Hecke algebras arising from types constructed by Roche.
${\mathrm {c-ind}}_U^G (\psi )$
corresponding to representations induced from the Borel subgroup. Their result is formulated in terms of Hecke algebras arising from types constructed by Roche.
For a general G, one does not have a complete theory of types and corresponding Hecke algebras, but there is a replacement: endomorphism algebras of pro-generators of Bernstein components.
It turns out that these algebras are more suited for the problem at hand. In more detail, let
![]() $P=MN$
be a parabolic subgroup of G, and let
$P=MN$
be a parabolic subgroup of G, and let
![]() $\sigma $
be an irreducible cuspidal representation of M. Let
$\sigma $
be an irreducible cuspidal representation of M. Let
![]() $M^{\circ }$
be the subgroup of M consisting of all
$M^{\circ }$
be the subgroup of M consisting of all
![]() $m\in M$
such that
$m\in M$
such that
![]() $|\chi (m)|=1$
for all smooth characters
$|\chi (m)|=1$
for all smooth characters
![]() $\chi : M \rightarrow {\mathbb C}^{\times }$
. Let
$\chi : M \rightarrow {\mathbb C}^{\times }$
. Let
![]() $\sigma _0$
be an irreducible summand of
$\sigma _0$
be an irreducible summand of
![]() $\sigma $
restricted to
$\sigma $
restricted to
![]() $M^{\circ }$
. Then
$M^{\circ }$
. Then
![]() $i_P^G( {\mathrm {c-ind}}^M_{M^{\circ }} (\sigma _0) )$
is a projective G-module generating a single Bernstein component. Here,
$i_P^G( {\mathrm {c-ind}}^M_{M^{\circ }} (\sigma _0) )$
is a projective G-module generating a single Bernstein component. Here,
![]() $i_P^G$
denotes normalized parabolic induction. Let
$i_P^G$
denotes normalized parabolic induction. Let
Observe that we have a natural inclusion
For every G-module
![]() $\pi $
,
$\pi $
,
is naturally a right
![]() ${\mathcal H}$
-module. The functor
${\mathcal H}$
-module. The functor
![]() $\mathfrak F$
is an equivalence between the Bernstein component generated by
$\mathfrak F$
is an equivalence between the Bernstein component generated by
![]() $i_P^G( {\mathrm {c-ind}}^M_{M^{\circ }} (\sigma _0) )$
and the category of right
$i_P^G( {\mathrm {c-ind}}^M_{M^{\circ }} (\sigma _0) )$
and the category of right
![]() ${\mathcal H}$
-modules.
${\mathcal H}$
-modules.
Now, assume that
![]() $\sigma $
is
$\sigma $
is
![]() $\psi $
-generic. Let
$\psi $
-generic. Let
It is not difficult to see, using Bernstein’s second adjointness, that
![]() $\Pi \cong \mathcal A $
, as
$\Pi \cong \mathcal A $
, as
![]() $\mathcal A$
-modules. Thus, understanding
$\mathcal A$
-modules. Thus, understanding
![]() $\Pi $
reduces to understanding
$\Pi $
reduces to understanding
![]() ${\mathcal H}$
-modules isomorphic to
${\mathcal H}$
-modules isomorphic to
![]() $\mathcal A$
. This was done for
$\mathcal A$
. This was done for
![]() $\mathrm {GL}_n$
in [Reference Chan and Savin11]. We extend this computation to
$\mathrm {GL}_n$
in [Reference Chan and Savin11]. We extend this computation to
![]() ${\mathcal H}$
for
${\mathcal H}$
for
![]() $G=\mathrm {SO}(2n+1,F)$
,
$G=\mathrm {SO}(2n+1,F)$
,
![]() $\mathrm {Sp}(2n,F)$
, and
$\mathrm {Sp}(2n,F)$
, and
![]() $\mathrm {O}(2n,F)$
. For classical groups, the algebra
$\mathrm {O}(2n,F)$
. For classical groups, the algebra
![]() ${\mathcal H}$
has been computed by Heiermann [Reference Heiermann17]; more recently, Solleveld [Reference Solleveld25] has studied the same algebra in a more general setting. If
${\mathcal H}$
has been computed by Heiermann [Reference Heiermann17]; more recently, Solleveld [Reference Solleveld25] has studied the same algebra in a more general setting. If
![]() $G=\mathrm {SO}(2n+1,F)$
,
$G=\mathrm {SO}(2n+1,F)$
,
![]() $\mathrm {Sp}(2n,F)$
, or
$\mathrm {Sp}(2n,F)$
, or
![]() $\mathrm {O}(2n,F)$
, it turns out that the algebra
$\mathrm {O}(2n,F)$
, it turns out that the algebra
![]() ${\mathcal H}$
is a tensor product of affine Hecke algebras, each of which is isomorphic to the Iwahori–Hecke algebra of
${\mathcal H}$
is a tensor product of affine Hecke algebras, each of which is isomorphic to the Iwahori–Hecke algebra of
![]() $\mathrm {GL}_k$
or to an algebra of type
$\mathrm {GL}_k$
or to an algebra of type
![]() $\tilde C_k$
with semisimple rank
$\tilde C_k$
with semisimple rank
![]() $k\leq n$
, with unequal parameters. (Note that we work with the full orthogonal group
$k\leq n$
, with unequal parameters. (Note that we work with the full orthogonal group
![]() $\mathrm {O}(2n)$
instead of
$\mathrm {O}(2n)$
instead of
![]() $\mathrm {SO}(2n)$
; this is because the case of
$\mathrm {SO}(2n)$
; this is because the case of
![]() $\mathrm {SO}(2n)$
is significantly more involved due to the complicated structure of the R-group [Reference Goldberg14].) Assume that
$\mathrm {SO}(2n)$
is significantly more involved due to the complicated structure of the R-group [Reference Goldberg14].) Assume that
![]() ${\mathcal H}$
corresponds to the affine type
${\mathcal H}$
corresponds to the affine type
![]() $\tilde C_n$
. The diagram has two special vertices, denoted by
$\tilde C_n$
. The diagram has two special vertices, denoted by
![]() $0$
and n. Corresponding to them, we have two finite subalgebras
$0$
and n. Corresponding to them, we have two finite subalgebras
![]() ${\mathcal H}_0$
and
${\mathcal H}_0$
and
![]() ${\mathcal H}_n$
of
${\mathcal H}_n$
of
![]() ${\mathcal H}$
. We prove that any
${\mathcal H}$
. We prove that any
![]() ${\mathcal H}$
-module isomorphic to
${\mathcal H}$
-module isomorphic to
![]() $\mathcal A$
is necessarily
$\mathcal A$
is necessarily
for a one-dimensional representation
![]() $\epsilon _0$
or
$\epsilon _0$
or
![]() $\epsilon _n$
. Here, we moved to more familiar language of left
$\epsilon _n$
. Here, we moved to more familiar language of left
![]() ${\mathcal H}$
-modules. This is harmless indeed, since
${\mathcal H}$
-modules. This is harmless indeed, since
![]() ${\mathcal H}$
is isomorphic to its opposite algebra; this follows from the Iwahori–Matsumoto relations. Finally, we determine precisely the isomorphism class of
${\mathcal H}$
is isomorphic to its opposite algebra; this follows from the Iwahori–Matsumoto relations. Finally, we determine precisely the isomorphism class of
![]() $\Pi $
.
$\Pi $
.
Next, we apply the classification of
![]() ${\mathcal H}$
-modules isomorphic to
${\mathcal H}$
-modules isomorphic to
![]() $\mathcal A$
to study the Gan–Gross–Prasad restriction problem from
$\mathcal A$
to study the Gan–Gross–Prasad restriction problem from
![]() $\mathrm {O}(m+1,F)$
to
$\mathrm {O}(m+1,F)$
to
![]() $\mathrm {O}(m,F)$
. Fix an irreducible supercuspidal representation of
$\mathrm {O}(m,F)$
. Fix an irreducible supercuspidal representation of
![]() $\mathrm {O}(m+1,F)$
. Then, for every maximal ideal
$\mathrm {O}(m+1,F)$
. Then, for every maximal ideal
![]() $\mathcal J$
in the Bernstein center of
$\mathcal J$
in the Bernstein center of
![]() $\mathrm {O}(m,F)$
, there exists at most one irreducible quotient annihilated by
$\mathrm {O}(m,F)$
, there exists at most one irreducible quotient annihilated by
![]() $\mathcal J$
. This is a generalization of a similar result for general linear groups where only Whittaker generic representations of
$\mathcal J$
. This is a generalization of a similar result for general linear groups where only Whittaker generic representations of
![]() $\mathrm {GL}(n)$
appear as quotients of supercuspidal representations of
$\mathrm {GL}(n)$
appear as quotients of supercuspidal representations of
![]() $\mathrm {GL}(n+1)$
.
$\mathrm {GL}(n+1)$
.
We finish this paper with an appendix where we show that
![]() $\mathcal {H}$
is isomorphic with the Hecke algebra arising from the type constructed by Stevens.
$\mathcal {H}$
is isomorphic with the Hecke algebra arising from the type constructed by Stevens.
2 Preliminaries
2.1 Notation
Throughout the paper, F will denote a non-Archimedean local field of residue characteristic q and uniformizer
![]() $\varpi $
, equipped with the absolute value
$\varpi $
, equipped with the absolute value
![]() $|\cdot |$
normalized in the usual way.
$|\cdot |$
normalized in the usual way.
We let G denote the special odd orthogonal group, the symplectic group, or the (full) even orthogonal group. If we want to emphasize the rank, we use
![]() $G_n$
to denote
$G_n$
to denote
![]() $\mathrm {SO}(2n+1,F)$
,
$\mathrm {SO}(2n+1,F)$
,
![]() $\mathrm {Sp}(2n,F)$
, or
$\mathrm {Sp}(2n,F)$
, or
![]() $\mathrm {O}(2n,F)$
. By
$\mathrm {O}(2n,F)$
. By
![]() $\text {Rep}(G)$
, we denote the category of smooth complex representations of G.
$\text {Rep}(G)$
, we denote the category of smooth complex representations of G.
For an arbitrary group H, we let
![]() $X(H)$
denote the group of complex characters of H.
$X(H)$
denote the group of complex characters of H.
2.2 Parabolic subgroups
If G is the disconnected group
![]() $\mathrm {O}(2n,F)$
, then, following [Reference Goldberg and Herb15], we consider only parabolic subgroups
$\mathrm {O}(2n,F)$
, then, following [Reference Goldberg and Herb15], we consider only parabolic subgroups
![]() $P=MN$
such that M has supercuspidal (modulo center) representations. Explicitly, this means that
$P=MN$
such that M has supercuspidal (modulo center) representations. Explicitly, this means that
however, we do not allow
![]() $n_0=1$
if
$n_0=1$
if
![]() $\mathrm {O}(2n,F)$
is split.
$\mathrm {O}(2n,F)$
is split.
2.3 Unramified characters
If M is a Levi subgroup of G, we let
![]() $M^{\circ } = \bigcap _{\chi } \ker |\chi |$
, the intersection taken over the set of all rational characters
$M^{\circ } = \bigcap _{\chi } \ker |\chi |$
, the intersection taken over the set of all rational characters
![]() $\chi : M \to F^{\times }$
. We say that a (complex) character
$\chi : M \to F^{\times }$
. We say that a (complex) character
![]() $\chi $
of M is unramified if it is trivial on
$\chi $
of M is unramified if it is trivial on
![]() $M^{\circ }$
; we let
$M^{\circ }$
; we let
![]() $X^{\text {nr}}(M)$
denote the group of all unramified characters on M. Then
$X^{\text {nr}}(M)$
denote the group of all unramified characters on M. Then
![]() $M/M^{\circ }$
is a free
$M/M^{\circ }$
is a free
![]() $\mathbb {Z}$
-module of finite rank, and the group
$\mathbb {Z}$
-module of finite rank, and the group
![]() $X^{\text {nr}}(M) = X(M/M^{\circ })$
has a natural structure of a complex affine variety. For any element
$X^{\text {nr}}(M) = X(M/M^{\circ })$
has a natural structure of a complex affine variety. For any element
![]() $m\in M$
, we denote by
$m\in M$
, we denote by
![]() $b_m$
the evaluation
$b_m$
the evaluation
![]() $\chi \mapsto \chi (m)$
.
$\chi \mapsto \chi (m)$
.
Now, let
![]() $\sigma $
be an irreducible cuspidal representation of M, and set
$\sigma $
be an irreducible cuspidal representation of M, and set
![]() $M^{\sigma } = \{m \in M : {}^m{\sigma } \cong \sigma \}$
. Then
$M^{\sigma } = \{m \in M : {}^m{\sigma } \cong \sigma \}$
. Then
![]() $M/M^{\sigma }$
is a finite abelian group and, abusing notation, we let
$M/M^{\sigma }$
is a finite abelian group and, abusing notation, we let
![]() $\mathcal {A}$
denote the ring of regular functions on the quotient variety
$\mathcal {A}$
denote the ring of regular functions on the quotient variety
![]() $X(M/M^{\circ })/X(M/M^{\sigma })$
. Since
$X(M/M^{\circ })/X(M/M^{\sigma })$
. Since
![]() $M^{\sigma }/M^{\circ }$
is once again a free
$M^{\sigma }/M^{\circ }$
is once again a free
![]() $\mathbb {Z}$
-module (of the same rank as
$\mathbb {Z}$
-module (of the same rank as
![]() $M/M^{\circ }$
), we have
$M/M^{\circ }$
), we have
![]() $\mathcal {A} \cong \mathbb {C}[M^{\sigma }/M^{\circ }]$
, by
$\mathcal {A} \cong \mathbb {C}[M^{\sigma }/M^{\circ }]$
, by
![]() $m \mapsto b_m$
. Furthermore, letting
$m \mapsto b_m$
. Furthermore, letting
![]() $\sigma _0$
denote an arbitrary irreducible constituent of
$\sigma _0$
denote an arbitrary irreducible constituent of
![]() $\sigma |_{M^{\circ }}$
, we have a canonical isomorphism
$\sigma |_{M^{\circ }}$
, we have a canonical isomorphism
![]() $\mathcal {A} \cong {\mathrm {End}}_M({\mathrm {c-ind}}_{M^{\circ }}^M \sigma _0)$
. Indeed, this follows from a simple application of Mackey theory. We refer the reader to [Reference Heiermann17, Sections 1.17 and 4] for additional details.
$\mathcal {A} \cong {\mathrm {End}}_M({\mathrm {c-ind}}_{M^{\circ }}^M \sigma _0)$
. Indeed, this follows from a simple application of Mackey theory. We refer the reader to [Reference Heiermann17, Sections 1.17 and 4] for additional details.
2.4 The Hecke algebra of a Bernstein component
If
![]() $\pi $
is an irreducible representation of G, there is a Levi subgroup M of G and an irreducible cuspidal representation
$\pi $
is an irreducible representation of G, there is a Levi subgroup M of G and an irreducible cuspidal representation
![]() $\sigma $
of M such that
$\sigma $
of M such that
![]() $\pi $
is (isomorphic to) a subquotient of
$\pi $
is (isomorphic to) a subquotient of
![]() $i_P^G(\sigma )$
. Here, P is a parabolic subgroup of G with a Levi component M. The pair
$i_P^G(\sigma )$
. Here, P is a parabolic subgroup of G with a Levi component M. The pair
![]() $(M,\sigma )$
is determined by
$(M,\sigma )$
is determined by
![]() $\pi $
up to conjugacy; we call
$\pi $
up to conjugacy; we call
![]() $(M,\sigma )$
the cuspidal support of
$(M,\sigma )$
the cuspidal support of
![]() $\pi $
.
$\pi $
.
We say that the two pairs
![]() $(M_1,\sigma _1)$
and
$(M_1,\sigma _1)$
and
![]() $(M_2,\sigma _2)$
as above are inertially equivalent if there exist an element
$(M_2,\sigma _2)$
as above are inertially equivalent if there exist an element
![]() $g\in G$
and an unramified character
$g\in G$
and an unramified character
![]() $\chi $
of
$\chi $
of
![]() $M_2$
such that
$M_2$
such that
This is an equivalence relation on the set of all pairs
![]() $(M,\sigma )$
. Given an equivalence class
$(M,\sigma )$
. Given an equivalence class
![]() $[(M,\sigma )]$
, we denote by
$[(M,\sigma )]$
, we denote by
![]() $\text {Rep}_{(M,\sigma )}(G)$
the full subcategory of
$\text {Rep}_{(M,\sigma )}(G)$
the full subcategory of
![]() $\text {Rep}(G)$
defined by the requirement that all irreducible subquotients of every object in
$\text {Rep}(G)$
defined by the requirement that all irreducible subquotients of every object in
![]() $\text {Rep}_{(M,\sigma )}(G)$
be supported within the inertial class
$\text {Rep}_{(M,\sigma )}(G)$
be supported within the inertial class
![]() $[(M,\sigma )]$
. A classic result of Bernstein then shows that the category
$[(M,\sigma )]$
. A classic result of Bernstein then shows that the category
![]() $\text {Rep}(G)$
decomposes as a direct product
$\text {Rep}(G)$
decomposes as a direct product
taken over the set of all inertial equivalence classes. We refer to
![]() $\text {Rep}_{(M,\sigma )}(G)$
as the Bernstein component attached to the pair
$\text {Rep}_{(M,\sigma )}(G)$
as the Bernstein component attached to the pair
![]() $(M,\sigma )$
. For a detailed discussion of the above results, see [Reference Bernstein3] or [Reference Bernstein4].
$(M,\sigma )$
. For a detailed discussion of the above results, see [Reference Bernstein3] or [Reference Bernstein4].
For each Bernstein component
![]() $\text {Rep}_{(M,\sigma )}(G)$
, one can construct a projective generator
$\text {Rep}_{(M,\sigma )}(G)$
, one can construct a projective generator
![]() $\Gamma _{(M,\sigma )}$
by setting
$\Gamma _{(M,\sigma )}$
by setting
Here,
![]() $\sigma _0$
is any irreducible component of the (semisimple) restriction
$\sigma _0$
is any irreducible component of the (semisimple) restriction
![]() $\sigma |_{M^{\circ }}$
. We now obtain a functor from the category
$\sigma |_{M^{\circ }}$
. We now obtain a functor from the category
![]() $\text {Rep}_{(M,\sigma )}(G)$
to the category of right
$\text {Rep}_{(M,\sigma )}(G)$
to the category of right
![]() ${\mathrm {End}}_G(\Gamma _{(M,\sigma )})$
-modules given by
${\mathrm {End}}_G(\Gamma _{(M,\sigma )})$
-modules given by
The fact that
![]() $\Gamma _{(M,\sigma )}$
is a projective generator implies that this is an equivalence of categories. This is [Reference Bernstein4, Lemma 22]; a detailed proof of this fact is also given in [Reference Roche, Cunningham and Nevins22, Theorem 1.5.3.1].
$\Gamma _{(M,\sigma )}$
is a projective generator implies that this is an equivalence of categories. This is [Reference Bernstein4, Lemma 22]; a detailed proof of this fact is also given in [Reference Roche, Cunningham and Nevins22, Theorem 1.5.3.1].
Given a Bernstein component attached to
![]() $\mathfrak {s} = (M,\sigma )$
, we use
$\mathfrak {s} = (M,\sigma )$
, we use
![]() $\mathcal {H}_{\mathfrak {s}}$
to denote
$\mathcal {H}_{\mathfrak {s}}$
to denote
![]() ${\mathrm {End}}_G(\Gamma _{\mathfrak {s}})$
and refer to it as the Hecke algebra attached to the component
${\mathrm {End}}_G(\Gamma _{\mathfrak {s}})$
and refer to it as the Hecke algebra attached to the component
![]() $\mathfrak {s}$
. Furthermore, for any
$\mathfrak {s}$
. Furthermore, for any
![]() $\pi \in \text {Rep}(G)$
, we let
$\pi \in \text {Rep}(G)$
, we let
![]() $\pi _{\mathfrak {s}}$
denote the corresponding
$\pi _{\mathfrak {s}}$
denote the corresponding
![]() $\mathcal {H}_{\mathfrak {s}}$
-module
$\mathcal {H}_{\mathfrak {s}}$
-module
![]() ${\mathrm {Hom}}(\Gamma _{\mathfrak {s}},\pi )$
.
${\mathrm {Hom}}(\Gamma _{\mathfrak {s}},\pi )$
.
Although we do not use it here, we point out that there is another highly useful approach to analyzing Bernstein components, based on the theory of types developed by Bushnell and Kutzko [Reference Bushnell and Kutzko8]. One can show that the Hecke algebra used by Bushnell and Kutzko is in fact isomorphic to the algebra
![]() $\mathcal {H}_{\mathfrak {s}}$
introduced above; we prove this fact in Appendix A. Therefore—for the purposes of this paper—the two approaches are equivalent.
$\mathcal {H}_{\mathfrak {s}}$
introduced above; we prove this fact in Appendix A. Therefore—for the purposes of this paper—the two approaches are equivalent.
2.5 Cuspidal representations
Here, we briefly recall some facts and introduce notation related to cuspidal representations of classical groups.
Let
![]() $\rho $
and
$\rho $
and
![]() $\tau $
be irreducible unitarizable cuspidal representations of
$\tau $
be irreducible unitarizable cuspidal representations of
![]() $\mathrm {GL}_k(F)$
and
$\mathrm {GL}_k(F)$
and
![]() $G_{n_0}$
, respectively. We consider the representation
$G_{n_0}$
, respectively. We consider the representation
![]() $\nu ^{\alpha }\rho \rtimes \tau $
, where
$\nu ^{\alpha }\rho \rtimes \tau $
, where
![]() $\alpha \in \mathbb {R}$
. Here, and throughout the paper, we use
$\alpha \in \mathbb {R}$
. Here, and throughout the paper, we use
![]() $\nu $
to denote the unramified character
$\nu $
to denote the unramified character
![]() $\lvert \det \rvert $
of the general linear group. If
$\lvert \det \rvert $
of the general linear group. If
![]() $\rho $
is not self-dual, the above representation never reduces. If
$\rho $
is not self-dual, the above representation never reduces. If
![]() $\rho $
is self-dual, then there exists a unique
$\rho $
is self-dual, then there exists a unique
![]() $\alpha \geq 0$
such that
$\alpha \geq 0$
such that
![]() $\nu ^{\alpha }\rho \rtimes \tau $
is reducible; we denote it by
$\nu ^{\alpha }\rho \rtimes \tau $
is reducible; we denote it by
![]() $\alpha _{\rho }$
.
$\alpha _{\rho }$
.
The number
![]() $\alpha _{\rho }$
has a natural description in terms of Langlands parameters. Let
$\alpha _{\rho }$
has a natural description in terms of Langlands parameters. Let
![]() $\phi $
be the L-parameter of
$\phi $
be the L-parameter of
![]() $\tau $
. Then
$\tau $
. Then
![]() $\phi $
decomposes into a direct sum of irreducible representations of
$\phi $
decomposes into a direct sum of irreducible representations of
![]() $W_F \times \text {SL}_2(\mathbb {C})$
. We view
$W_F \times \text {SL}_2(\mathbb {C})$
. We view
![]() $\rho $
as a representation of
$\rho $
as a representation of
![]() $W_F$
; we say that it is of the same type as
$W_F$
; we say that it is of the same type as
![]() $\phi $
if the corresponding
$\phi $
if the corresponding
![]() $W_F$
-representation factors through a group of the same type (orthogonal/symplectic) as
$W_F$
-representation factors through a group of the same type (orthogonal/symplectic) as
![]() $\phi $
. Letting
$\phi $
. Letting
![]() $S_a$
denote the (unique) irreducible algebraic a-dimensional representation of
$S_a$
denote the (unique) irreducible algebraic a-dimensional representation of
![]() $\text {SL}_2(\mathbb {C})$
, we now set
$\text {SL}_2(\mathbb {C})$
, we now set
If the above set is empty, we let
 $$\begin{align*}a_{\rho} = \begin{cases} -1, \quad &\text{if } \rho \text{ is of the same type as }\phi,\\ 0, \quad &\text{otherwise}. \end{cases} \end{align*}$$
$$\begin{align*}a_{\rho} = \begin{cases} -1, \quad &\text{if } \rho \text{ is of the same type as }\phi,\\ 0, \quad &\text{otherwise}. \end{cases} \end{align*}$$
With this description of
![]() $a_{\rho }$
, we have
$a_{\rho }$
, we have
![]() $\alpha _{\rho } = \frac {a_{\rho }+1}{2}$
.
$\alpha _{\rho } = \frac {a_{\rho }+1}{2}$
.
2.6 The structure of the Hecke algebra
We retain the notation
![]() $\rho , \tau $
, and
$\rho , \tau $
, and
![]() $G_n$
from the previous subsection, and consider the cuspidal component
$G_n$
from the previous subsection, and consider the cuspidal component
![]() $\mathfrak {s}$
attached to the representation
$\mathfrak {s}$
attached to the representation
of the Levi subgroup
![]() $M = \mathrm {GL}_k(F) \times \dotsb \times \mathrm {GL}_k(F) \times G_{n_0}$
in
$M = \mathrm {GL}_k(F) \times \dotsb \times \mathrm {GL}_k(F) \times G_{n_0}$
in
![]() $G_{N}$
, where
$G_{N}$
, where
![]() $N = nk+n_0$
. In the rest of the paper, we restrict our attention to cuspidal components of the above form. This does not present a significant loss of generality, since the Hecke algebra of a general cuspidal component is the product of algebras corresponding to the components described above. To simplify notation, we set
$N = nk+n_0$
. In the rest of the paper, we restrict our attention to cuspidal components of the above form. This does not present a significant loss of generality, since the Hecke algebra of a general cuspidal component is the product of algebras corresponding to the components described above. To simplify notation, we set
![]() $\mathcal {H} = \mathcal {H}_{\mathfrak {s}}$
.
$\mathcal {H} = \mathcal {H}_{\mathfrak {s}}$
.
The structure of the Hecke algebra
![]() $\mathcal {H}$
has been completely described by Heiermann [Reference Heiermann16, Reference Heiermann17]. In his work, Heiermann shows that
$\mathcal {H}$
has been completely described by Heiermann [Reference Heiermann16, Reference Heiermann17]. In his work, Heiermann shows that
![]() $\mathcal {H}$
is a Hecke algebra with parameters (the type of the algebra and the parameters depending on the specifics of the given case). When the component in question is of the form described above, we have three distinct cases, which we now summarize. For basic definitions and results on Hecke algebras with parameters, we refer to the work of Lusztig [Reference Lusztig19].
$\mathcal {H}$
is a Hecke algebra with parameters (the type of the algebra and the parameters depending on the specifics of the given case). When the component in question is of the form described above, we have three distinct cases, which we now summarize. For basic definitions and results on Hecke algebras with parameters, we refer to the work of Lusztig [Reference Lusztig19].
In what follows, we let t denote the order of the (finite) group
![]() $\{\chi \in X^{\text {nr}}(\mathrm {GL}_k(F)): \rho \otimes \chi \cong \rho \}$
. In all three cases, the commutative algebra
$\{\chi \in X^{\text {nr}}(\mathrm {GL}_k(F)): \rho \otimes \chi \cong \rho \}$
. In all three cases, the commutative algebra
![]() $\mathcal {A}$
(see Section 2.3) is a subalgebra of
$\mathcal {A}$
(see Section 2.3) is a subalgebra of
![]() $\mathcal {H}$
. In the present setting, the rank of the free module
$\mathcal {H}$
. In the present setting, the rank of the free module
![]() $M^{\sigma }/M^{\circ }$
is equal to n. We can thus identify
$M^{\sigma }/M^{\circ }$
is equal to n. We can thus identify
![]() $\mathcal {A} \cong \mathbb {C}[M^{\sigma }/M^{\circ }]$
with the algebra of Laurent polynomials
$\mathcal {A} \cong \mathbb {C}[M^{\sigma }/M^{\circ }]$
with the algebra of Laurent polynomials
![]() $\mathbb {C}[X_1^{\pm },\dotsc ,X_n^{\pm }]$
. We fix this isomorphism explicitly: For
$\mathbb {C}[X_1^{\pm },\dotsc ,X_n^{\pm }]$
. We fix this isomorphism explicitly: For
![]() $i = 1, \dotsc , n$
, let
$i = 1, \dotsc , n$
, let
![]() $h_i$
be the element of M which is equal to
$h_i$
be the element of M which is equal to
![]() $\text {diag}(\varpi ,1,\dotsc ,1)$
on the ith
$\text {diag}(\varpi ,1,\dotsc ,1)$
on the ith
![]() $\mathrm {GL}$
factor, and equal to the identity elsewhere. Then
$\mathrm {GL}$
factor, and equal to the identity elsewhere. Then
![]() $X_i = b_{h_i}^t$
. The three cases are:
$X_i = b_{h_i}^t$
. The three cases are:
-
(i) No representation of the form
 $\rho \otimes \chi $
with
$\rho \otimes \chi $
with
 $\chi \in X^{\text {nr}}(\mathrm{GL}_{k}(F))$
is self-dual.
$\chi \in X^{\text {nr}}(\mathrm{GL}_{k}(F))$
is self-dual.In this case, the algebra
 $\mathcal {H}$
is described by an affine Coxeter diagram of type
$\mathcal {H}$
is described by an affine Coxeter diagram of type
 $\tilde {A}_{n-1}$
with equal parameters t. In other words, it is isomorphic to the algebra
$\tilde {A}_{n-1}$
with equal parameters t. In other words, it is isomorphic to the algebra
 $\mathcal {H}_n$
described in [Reference Chan and Savin11]: There are elements
$\mathcal {H}_n$
described in [Reference Chan and Savin11]: There are elements
 $T_1, \dotsc , T_{n-1}$
which satisfy the quadratic relation and commutation relations
$T_1, \dotsc , T_{n-1}$
which satisfy the quadratic relation and commutation relations $$\begin{align*}(T_i + 1)(T_i - q^t) = 0, \quad i = 1,\dotsc, n-1 \end{align*}$$
where
$$\begin{align*}(T_i + 1)(T_i - q^t) = 0, \quad i = 1,\dotsc, n-1 \end{align*}$$
where $$\begin{align*}T_i f - f^{s_i}T_i = (q^t-1) \frac{f - f^{s_i}}{1 - X_{i+1}/X_i}, \quad i = 1,\dotsc, n-1, \end{align*}$$
$$\begin{align*}T_i f - f^{s_i}T_i = (q^t-1) \frac{f - f^{s_i}}{1 - X_{i+1}/X_i}, \quad i = 1,\dotsc, n-1, \end{align*}$$
 $f^{s_i}$
is obtained from
$f^{s_i}$
is obtained from
 $f \in \mathcal {A}$
by swapping
$f \in \mathcal {A}$
by swapping
 $X_i$
and
$X_i$
and
 $X_{i+1}$
.
$X_{i+1}$
.
In the two remaining cases, there is an unramified character
![]() $\chi $
such that
$\chi $
such that
![]() $\rho \otimes \chi $
is self-dual. Without loss of generality, we may assume that
$\rho \otimes \chi $
is self-dual. Without loss of generality, we may assume that
![]() $\rho $
is self-dual. Then, up to isomorphism, there is a unique representation of the form
$\rho $
is self-dual. Then, up to isomorphism, there is a unique representation of the form
![]() $\rho \otimes \chi \ncong \rho $
which is also self-dual; we denote it by
$\rho \otimes \chi \ncong \rho $
which is also self-dual; we denote it by
![]() $\rho ^-$
. We set
$\rho ^-$
. We set
![]() $\alpha = \alpha _{\rho }$
and
$\alpha = \alpha _{\rho }$
and
![]() $\beta = \alpha _{\rho ^-}$
(see Section 2.5 for notation). Since the situation is symmetric, we may (and will) assume that
$\beta = \alpha _{\rho ^-}$
(see Section 2.5 for notation). Since the situation is symmetric, we may (and will) assume that
![]() $\alpha \geq \beta $
. The description of
$\alpha \geq \beta $
. The description of
![]() $\mathcal {H}$
now involves two additional operators
$\mathcal {H}$
now involves two additional operators
![]() $T_0$
and
$T_0$
and
![]() $T_n$
(see Remark 2.1). We have the following two cases:
$T_n$
(see Remark 2.1). We have the following two cases:
-
(ii)
 $\alpha = \beta = 0$
.
$\alpha = \beta = 0$
.In this case,
 $\mathcal {H}$
is described by an affine Coxeter diagram of type
$\mathcal {H}$
is described by an affine Coxeter diagram of type
 $\tilde {C}_n$
: The nodes correspond to operators
$\tilde {C}_n$
: The nodes correspond to operators
 $T_0, \dotsc , T_n$
which satisfy the quadratic relations and the braid relations as prescribed by the diagram. The commutation relations for
$T_0, \dotsc , T_n$
which satisfy the quadratic relations and the braid relations as prescribed by the diagram. The commutation relations for $$\begin{align*}T_0^2 = 1, \quad T_n^2 = 1, \quad (T_i+1)(T_i-q^t) = 0\quad \text{for }i = 1, \dotsc, n-1, \end{align*}$$
$$\begin{align*}T_0^2 = 1, \quad T_n^2 = 1, \quad (T_i+1)(T_i-q^t) = 0\quad \text{for }i = 1, \dotsc, n-1, \end{align*}$$
 $T_i, i=1,\dotsc , n-1$
, are the same as in Case (i), whereas
$T_i, i=1,\dotsc , n-1$
, are the same as in Case (i), whereas
 $T_n$
satisfies with
$T_n$
satisfies with $$\begin{align*}fT_n - T_nf^{\vee} = 0 \end{align*}$$
$$\begin{align*}fT_n - T_nf^{\vee} = 0 \end{align*}$$
 $f^{\vee }(X_1,\dotsc ,X_{n-1},X_n) = f(X_1,\dotsc ,X_{n-1},1/X_n)$
.
$f^{\vee }(X_1,\dotsc ,X_{n-1},X_n) = f(X_1,\dotsc ,X_{n-1},1/X_n)$
.
-
(iii)
 $\alpha> 0$
.
$\alpha> 0$
.In this case,
 $\mathcal {H}$
is described by an affine Coxeter diagram of type
$\mathcal {H}$
is described by an affine Coxeter diagram of type
 $\tilde {C}_n$
: Here,
$\tilde {C}_n$
: Here,
 $s = t(\alpha -\beta )$
and
$s = t(\alpha -\beta )$
and
 $r = t(\alpha + \beta )$
. Again, the nodes correspond to operators
$r = t(\alpha + \beta )$
. Again, the nodes correspond to operators
 $T_0, \dotsc , T_n$
which satisfy quadratic relations analogous to those in Case (ii), along with the braid relations. The commutation relations for
$T_0, \dotsc , T_n$
which satisfy quadratic relations analogous to those in Case (ii), along with the braid relations. The commutation relations for
 $T_i, i=1,\dotsc , n-1$
, are the same as in Case (i), whereas
$T_i, i=1,\dotsc , n-1$
, are the same as in Case (i), whereas
 $T_n$
satisfies
$T_n$
satisfies  $$\begin{align*}fT_n - T_nf^{\vee} = \left((q^r-1) + \frac{1}{X_n}(\sqrt{q}^{r+s}-\sqrt{q}^{r-s})\right)\frac{f - f^{\vee}}{1-1/X_n^2}. \end{align*}$$
$$\begin{align*}fT_n - T_nf^{\vee} = \left((q^r-1) + \frac{1}{X_n}(\sqrt{q}^{r+s}-\sqrt{q}^{r-s})\right)\frac{f - f^{\vee}}{1-1/X_n^2}. \end{align*}$$
Cases (i)–(iii) correspond to Cases (I)–(III) listed in [Reference Heiermann16, Section 3.1]. The above results are collected in Section 3.4 of [Reference Heiermann16]. We take a moment to explain the situation in the even orthogonal case. Papers [Reference Heiermann16, Reference Heiermann17] do not treat the full orthogonal group; rather, they contain results about the special orthogonal group
![]() $\mathrm {SO}(2n)$
. In the special orthogonal case, there is a nontrivial R-group (see [Reference Goldberg14]) which complicates the structure of the Hecke algebra; this was ultimately worked out by Heiermann in [Reference Heiermann18]. Because of this, we choose to work with
$\mathrm {SO}(2n)$
. In the special orthogonal case, there is a nontrivial R-group (see [Reference Goldberg14]) which complicates the structure of the Hecke algebra; this was ultimately worked out by Heiermann in [Reference Heiermann18]. Because of this, we choose to work with
![]() $\mathrm {O}(2n)$
instead. This is indeed justified: Annex A of [Reference Heiermann18] shows that the results of [Reference Heiermann16, Reference Heiermann17] generalize to the full orthogonal case.
$\mathrm {O}(2n)$
instead. This is indeed justified: Annex A of [Reference Heiermann18] shows that the results of [Reference Heiermann16, Reference Heiermann17] generalize to the full orthogonal case.
A detailed construction of the operators
![]() $T_i$
(starting from standard intertwining operators) is the subject matter of [Reference Heiermann17]; we do not need the details here, except in a special case discussed in the final part of Section 3.2. To facilitate the comparison of the above summary to the works of Heiermann [Reference Heiermann16–Reference Heiermann18], we point out the ways in which our summary deviates from them.
$T_i$
(starting from standard intertwining operators) is the subject matter of [Reference Heiermann17]; we do not need the details here, except in a special case discussed in the final part of Section 3.2. To facilitate the comparison of the above summary to the works of Heiermann [Reference Heiermann16–Reference Heiermann18], we point out the ways in which our summary deviates from them.
Remark 2.1
-
(a) The explicit isomorphism
 $\mathbb {C}[M^{\sigma }/M^{\circ }] \cong \mathbb {C}[X_1^{\pm },\dotsc ,X_n^{\pm }]$
we use is different than the one used in [Reference Heiermann16]; there, Heiermann sets
$\mathbb {C}[M^{\sigma }/M^{\circ }] \cong \mathbb {C}[X_1^{\pm },\dotsc ,X_n^{\pm }]$
we use is different than the one used in [Reference Heiermann16]; there, Heiermann sets
 $X_i = b_{h_ih_{i+1}^{-1}}^t$
for
$X_i = b_{h_ih_{i+1}^{-1}}^t$
for
 ${i = 1, \dotsc , n-1}$
(and, in Case (ii),
${i = 1, \dotsc , n-1}$
(and, in Case (ii),
 $X_n = b_{h_{n-1}h_{n}}^t$
).
$X_n = b_{h_{n-1}h_{n}}^t$
). -
(b) The operator
 $T_0$
which appears in Cases (ii) and (iii) above is not needed to describe
$T_0$
which appears in Cases (ii) and (iii) above is not needed to describe
 $\mathcal {H}$
, and is therefore not used in [Reference Heiermann16, Reference Heiermann17]. To be precise, the Hecke algebra is generated over
$\mathcal {H}$
, and is therefore not used in [Reference Heiermann16, Reference Heiermann17]. To be precise, the Hecke algebra is generated over
 $\mathcal {A}$
by the operators
$\mathcal {A}$
by the operators
 $T_1,\dotsc ,T_n$
and determined by the quadratic and braid relations they satisfy, along with the commutation relations listed above. Each of the operators
$T_1,\dotsc ,T_n$
and determined by the quadratic and braid relations they satisfy, along with the commutation relations listed above. Each of the operators
 $T_1,\dotsc , T_n$
corresponds to a simple reflection in the Weyl group, whereas the operator
$T_1,\dotsc , T_n$
corresponds to a simple reflection in the Weyl group, whereas the operator
 $T_0$
corresponds to the reflection given by the (in this case, unique) minimal element of the root system (see [Reference Lusztig19, Section 1.4]). In fact, we define
$T_0$
corresponds to the reflection given by the (in this case, unique) minimal element of the root system (see [Reference Lusztig19, Section 1.4]). In fact, we define
 $T_0$
by setting where
$T_0$
by setting where $$\begin{align*}T_0 = \sqrt{q}^{s+2t(n-1)+r}X_1T_w^{-1}, \end{align*}$$
$$\begin{align*}T_0 = \sqrt{q}^{s+2t(n-1)+r}X_1T_w^{-1}, \end{align*}$$
 $T_w = T_1\dotsb T_{n-1}T_nT_{n-1}\dotsb T_1$
(see [Reference Lusztig19, Sections 2.8 and 3.3]). We use
$T_w = T_1\dotsb T_{n-1}T_nT_{n-1}\dotsb T_1$
(see [Reference Lusztig19, Sections 2.8 and 3.3]). We use
 $T_0$
out of convenience, as it allows a more symmetric description of certain
$T_0$
out of convenience, as it allows a more symmetric description of certain
 $\mathcal {H}$
-modules.
$\mathcal {H}$
-modules.
-
(c) The description of
 $\mathcal {H}$
in Case (ii) differs from the one given in [Reference Heiermann16], which views
$\mathcal {H}$
in Case (ii) differs from the one given in [Reference Heiermann16], which views
 $T_n$
as the nontrivial element of the R-group. However, one can verify that the description we use is equivalent. With our description, (ii) can be viewed as a special case of (iii) (with
$T_n$
as the nontrivial element of the R-group. However, one can verify that the description we use is equivalent. With our description, (ii) can be viewed as a special case of (iii) (with
 $r = s = 0$
); however, since our results in (ii) require additional analysis, we still state the two cases separately.
$r = s = 0$
); however, since our results in (ii) require additional analysis, we still state the two cases separately.
2.7 Generic representations
We recall only the most basic facts here; a general reference is, e.g., [Reference Shahidi24].
Assume that G is split, and let U is be a maximal unipotent subgroup of G. Fix a nondegenerate character
![]() $\psi $
of U. Recall that a character of U is said to be nondegenerate if it is nontrivial on every root subgroup corresponding to a simple root. We say that a representation
$\psi $
of U. Recall that a character of U is said to be nondegenerate if it is nontrivial on every root subgroup corresponding to a simple root. We say that a representation
![]() $(\pi ,V)$
of G is
$(\pi ,V)$
of G is
![]() $\psi $
-generic if there exists a so-called Whittaker functional—that is, a linear functional
$\psi $
-generic if there exists a so-called Whittaker functional—that is, a linear functional
![]() $L: V\to \mathbb {C}$
such that
$L: V\to \mathbb {C}$
such that
The key fact we use throughout is that the space of Whittaker functionals is at most one-dimensional. However, this fact does not hold for the disconnected
![]() $\mathrm {O}(2n, F)$
, and we need to adjust the definition of Whittaker character as follows. In this case, the Levi factor of the normalizer of U in
$\mathrm {O}(2n, F)$
, and we need to adjust the definition of Whittaker character as follows. In this case, the Levi factor of the normalizer of U in
![]() $\mathrm {O}(2n, F)$
is
$\mathrm {O}(2n, F)$
is
![]() $\mathrm {GL}_1(F) \times \cdots \times \mathrm {GL}_1(F) \times \mathrm {O}(2, F)$
and there exists
$\mathrm {GL}_1(F) \times \cdots \times \mathrm {GL}_1(F) \times \mathrm {O}(2, F)$
and there exists
![]() $\alpha \in \mathrm {O}(2,F) \setminus \mathrm {SO}(2,F)$
normalizing
$\alpha \in \mathrm {O}(2,F) \setminus \mathrm {SO}(2,F)$
normalizing
![]() $\psi $
. Observe that the order of
$\psi $
. Observe that the order of
![]() $\alpha $
is 2. We extend
$\alpha $
is 2. We extend
![]() $\psi $
to a character
$\psi $
to a character
![]() $\tilde \psi $
of
$\tilde \psi $
of
![]() $\tilde U= U\rtimes \langle \alpha \rangle $
by
$\tilde U= U\rtimes \langle \alpha \rangle $
by
![]() $\tilde \psi (\alpha )=1$
. With this extension, the space of Whittaker functionals for any irreducible representation of
$\tilde \psi (\alpha )=1$
. With this extension, the space of Whittaker functionals for any irreducible representation of
![]() $\mathrm {O}(2n, F)$
is at most one-dimensional.
$\mathrm {O}(2n, F)$
is at most one-dimensional.
Now, let
![]() $P=MN$
be a parabolic subgroup of G. If
$P=MN$
be a parabolic subgroup of G. If
![]() $\sigma $
is an irreducible generic representation of M, then one can construct a Whittaker functional on
$\sigma $
is an irreducible generic representation of M, then one can construct a Whittaker functional on
![]() $i_P^G\sigma $
(see [Reference Shahidi24, Proposition 3.1] and equation (3.11)); in other words, the induced representation is
$i_P^G\sigma $
(see [Reference Shahidi24, Proposition 3.1] and equation (3.11)); in other words, the induced representation is
![]() $\psi $
-generic as well. We use this fact later, in Section 3.2.
$\psi $
-generic as well. We use this fact later, in Section 3.2.
3 The Gelfand–Graev representation
Continuing with split G, let U be a maximal unipotent subgroup of G and fix a nondegenerate character
![]() $\psi : U \to \mathbb {C}^{\times }$
. The Gelfand–Graev representation of G is the compactly induced representation
$\psi : U \to \mathbb {C}^{\times }$
. The Gelfand–Graev representation of G is the compactly induced representation
![]() ${\mathrm {c-ind}}_U^G(\psi )$
. However, if
${\mathrm {c-ind}}_U^G(\psi )$
. However, if
![]() $G=\mathrm {O}(2n,F)$
, the pair
$G=\mathrm {O}(2n,F)$
, the pair
![]() $(U,\psi )$
is replaced by the pair
$(U,\psi )$
is replaced by the pair
![]() $(\tilde U, \tilde \psi )$
in this definition. With this modification for
$(\tilde U, \tilde \psi )$
in this definition. With this modification for
![]() $\mathrm {O}(2n,F)$
in mind, the Gelfand–Graev representation is the “universal”
$\mathrm {O}(2n,F)$
in mind, the Gelfand–Graev representation is the “universal”
![]() $\psi $
-generic representation: Every
$\psi $
-generic representation: Every
![]() $\psi $
-generic representation of G appears as a quotient (with multiplicity one).
$\psi $
-generic representation of G appears as a quotient (with multiplicity one).
From this point on, we assume that the cuspidal representation
![]() $\tau $
—used to define the Bernstein component
$\tau $
—used to define the Bernstein component
![]() $\mathfrak {s}$
in Section 2.6—is generic. We let
$\mathfrak {s}$
in Section 2.6—is generic. We let
![]() $\Pi $
denote
$\Pi $
denote
![]() $({\mathrm {c-ind}}_U^G(\psi ))$
viewed as an
$({\mathrm {c-ind}}_U^G(\psi ))$
viewed as an
![]() $\mathcal {H}$
-module. Our goal is to determine the structure of
$\mathcal {H}$
-module. Our goal is to determine the structure of
![]() $\Pi $
.
$\Pi $
.
We begin by investigating the structure of
![]() $\Pi $
as an
$\Pi $
as an
![]() $\mathcal {A}$
-module. We point out that the proof of the following proposition applies, without modification, to any split reductive p-adic group.
$\mathcal {A}$
-module. We point out that the proof of the following proposition applies, without modification, to any split reductive p-adic group.
Proposition 3.1 As
![]() $\mathcal {A}$
-modules, we have
$\mathcal {A}$
-modules, we have
![]() $\Pi \cong \mathcal {A}$
.
$\Pi \cong \mathcal {A}$
.
Proof The
![]() $\mathcal {H}$
-module
$\mathcal {H}$
-module
![]() $\Pi $
is given by
$\Pi $
is given by
![]() ${\mathrm {Hom}}_G(\Gamma _{\mathfrak {s}},{\mathrm {c-ind}}_U^G(\psi ))$
, where
${\mathrm {Hom}}_G(\Gamma _{\mathfrak {s}},{\mathrm {c-ind}}_U^G(\psi ))$
, where
![]() $\Gamma _{\mathfrak {s}} = i_P^G({\mathrm {c-ind}}_{M^{\circ }}^M(\sigma _0))$
. Recall that
$\Gamma _{\mathfrak {s}} = i_P^G({\mathrm {c-ind}}_{M^{\circ }}^M(\sigma _0))$
. Recall that
![]() $\sigma _0$
was taken to be an arbitrary irreducible constituent of
$\sigma _0$
was taken to be an arbitrary irreducible constituent of
![]() $\sigma |_{M^{\circ }}$
. However, having now fixed the Whittaker datum for M (and thus for
$\sigma |_{M^{\circ }}$
. However, having now fixed the Whittaker datum for M (and thus for
![]() $M^{\circ }$
), there exists a unique irreducible summand of
$M^{\circ }$
), there exists a unique irreducible summand of
![]() $\sigma |_{M^{\circ }}$
which is
$\sigma |_{M^{\circ }}$
which is
![]() $\psi $
-generic. Thus, from now on, we assume that
$\psi $
-generic. Thus, from now on, we assume that
![]() $\sigma _0$
is this unique
$\sigma _0$
is this unique
![]() $\psi $
-generic constituent of
$\psi $
-generic constituent of
![]() $\sigma |_{M^{\circ }}$
.
$\sigma |_{M^{\circ }}$
.
To view
![]() $\Pi $
as an
$\Pi $
as an
![]() $\mathcal {A}= {\mathrm {End}}_M({\mathrm {c-ind}}_{M^{\circ }}^M(\sigma _0))$
-module, we use the Bernstein version of Frobenius reciprocity:
$\mathcal {A}= {\mathrm {End}}_M({\mathrm {c-ind}}_{M^{\circ }}^M(\sigma _0))$
-module, we use the Bernstein version of Frobenius reciprocity:
 $$\begin{align*}\Pi &= {\mathrm{Hom}}_G( i_P^G({\mathrm{c-ind}}_{M^{\circ}}^M(\sigma_0)),{\mathrm{c-ind}}_U^G(\psi)) \\ & = {\mathrm{Hom}}_M( {\mathrm{c-ind}}_{M^{\circ}}^M(\sigma_0), r_{\overline{N}}({\mathrm{c-ind}}_U^G(\psi))); \end{align*}$$
$$\begin{align*}\Pi &= {\mathrm{Hom}}_G( i_P^G({\mathrm{c-ind}}_{M^{\circ}}^M(\sigma_0)),{\mathrm{c-ind}}_U^G(\psi)) \\ & = {\mathrm{Hom}}_M( {\mathrm{c-ind}}_{M^{\circ}}^M(\sigma_0), r_{\overline{N}}({\mathrm{c-ind}}_U^G(\psi))); \end{align*}$$
here,
![]() $r_{\overline {N}}$
denotes the Jacquet functor with respect to
$r_{\overline {N}}$
denotes the Jacquet functor with respect to
![]() $\overline {P}=M\overline {N}$
, the parabolic opposite to P.
$\overline {P}=M\overline {N}$
, the parabolic opposite to P.
We now use the fact that
![]() $ r_{\overline {N}}({\mathrm {c-ind}}_U^G(\psi ))$
is isomorphic to the Gelfand–Graev representation of M,
$ r_{\overline {N}}({\mathrm {c-ind}}_U^G(\psi ))$
is isomorphic to the Gelfand–Graev representation of M,
![]() ${\mathrm {c-ind}}_{U\cap M}^M(\psi )$
(see [Reference Bushnell and Henniart6, Section 2.2]). Furthermore, with the above choice of
${\mathrm {c-ind}}_{U\cap M}^M(\psi )$
(see [Reference Bushnell and Henniart6, Section 2.2]). Furthermore, with the above choice of
![]() $\sigma _0$
, the representation
$\sigma _0$
, the representation
![]() ${\mathrm {c-ind}}_{M^{\circ }}^M(\sigma _0)$
is precisely the sum of all maximal
${\mathrm {c-ind}}_{M^{\circ }}^M(\sigma _0)$
is precisely the sum of all maximal
![]() $({}^m\sigma _0)$
-isotypic components of
$({}^m\sigma _0)$
-isotypic components of
![]() ${\mathrm {c-ind}}_{U\cap M}^M(\psi )$
, where
${\mathrm {c-ind}}_{U\cap M}^M(\psi )$
, where
![]() ${}^m\sigma _0$
ranges over the set of all M-conjugates of
${}^m\sigma _0$
ranges over the set of all M-conjugates of
![]() $\sigma _0$
. Indeed,
$\sigma _0$
. Indeed,
![]() ${\mathrm {c-ind}}_{U\cap M}^M(\psi )$
is itself induced from the Gelfand–Graev representation of
${\mathrm {c-ind}}_{U\cap M}^M(\psi )$
is itself induced from the Gelfand–Graev representation of
![]() $M^{\circ }$
,
$M^{\circ }$
,
![]() ${\mathrm {c-ind}}_{U\cap M}^{M^{\circ }}(\psi )$
. Since
${\mathrm {c-ind}}_{U\cap M}^{M^{\circ }}(\psi )$
. Since
![]() $\sigma _0$
appears with multiplicity one, and no other m-conjugate of
$\sigma _0$
appears with multiplicity one, and no other m-conjugate of
![]() $\sigma _0$
is generic, we have
$\sigma _0$
is generic, we have
![]() ${\mathrm {c-ind}}_{U\cap M}^{M^{\circ }}(\psi ) \cong \sigma _0 \oplus \sigma _0^{\bot }$
, where
${\mathrm {c-ind}}_{U\cap M}^{M^{\circ }}(\psi ) \cong \sigma _0 \oplus \sigma _0^{\bot }$
, where
![]() $\sigma _0^{\bot }$
is a representation which contains no M-conjugate of
$\sigma _0^{\bot }$
is a representation which contains no M-conjugate of
![]() $\sigma _0$
. Inducing to M, we get
$\sigma _0$
. Inducing to M, we get
![]() ${\mathrm {c-ind}}_{U\cap M}^M(\psi ) = {\mathrm {c-ind}}_{M^{\circ }}^M(\sigma _0) \oplus {\mathrm {c-ind}}_{M^{\circ }}^M(\sigma _0^{\bot })$
, which proves the above claim about isotypic components. Thus, viewed as an
${\mathrm {c-ind}}_{U\cap M}^M(\psi ) = {\mathrm {c-ind}}_{M^{\circ }}^M(\sigma _0) \oplus {\mathrm {c-ind}}_{M^{\circ }}^M(\sigma _0^{\bot })$
, which proves the above claim about isotypic components. Thus, viewed as an
![]() $\mathcal {A}$
-module,
$\mathcal {A}$
-module,
![]() $\Pi $
is isomorphic to
$\Pi $
is isomorphic to
 $$ \begin{align*} & {\mathrm{Hom}}_M( {\mathrm{c-ind}}_{M^{\circ}}^M(\sigma_0), r_{\overline{N}}({\mathrm{c-ind}}_U^G(\psi))) \\ & \quad = {\mathrm{Hom}}_M( {\mathrm{c-ind}}_{M^{\circ}}^M(\sigma_0), {\mathrm{c-ind}}_{U\cap M}^M(\psi))\\ & \quad = {\mathrm{Hom}}_M( {\mathrm{c-ind}}_{M^{\circ}}^M(\sigma_0), {\mathrm{c-ind}}_{M^{\circ}}^M(\sigma_0)) = \mathcal{A}. \\[-34pt] \end{align*} $$
$$ \begin{align*} & {\mathrm{Hom}}_M( {\mathrm{c-ind}}_{M^{\circ}}^M(\sigma_0), r_{\overline{N}}({\mathrm{c-ind}}_U^G(\psi))) \\ & \quad = {\mathrm{Hom}}_M( {\mathrm{c-ind}}_{M^{\circ}}^M(\sigma_0), {\mathrm{c-ind}}_{U\cap M}^M(\psi))\\ & \quad = {\mathrm{Hom}}_M( {\mathrm{c-ind}}_{M^{\circ}}^M(\sigma_0), {\mathrm{c-ind}}_{M^{\circ}}^M(\sigma_0)) = \mathcal{A}. \\[-34pt] \end{align*} $$
Remark 3.2 We point out that the above differs from the proof of the analogous statement in [Reference Chan and Savin11]. It is shown there that any
![]() $\mathcal {H}$
-module
$\mathcal {H}$
-module
![]() $\Pi $
which is
$\Pi $
which is
-
(i) projective;
-
(ii) finitely generated; and which satisfies
-
(iii)
 $\dim {\mathrm {Hom}}_{\mathcal {H}}(\Pi ,\pi ) \leq 1$
for any principal series representation
$\dim {\mathrm {Hom}}_{\mathcal {H}}(\Pi ,\pi ) \leq 1$
for any principal series representation
 $\pi $
$\pi $
is isomorphic to
![]() $\mathcal {A}$
when viewed as an
$\mathcal {A}$
when viewed as an
![]() $\mathcal {A}$
-module (see [Reference Chan and Savin11, Lemmas 2.2 and 2.3]). The Gelfand–Graev representation can be shown to satisfy properties (i)–(iii): Property (i) is provided by Corollary 8.6 of [Reference Chan and Savin11]; (ii) is proved in [Reference Bushnell and Henniart6], and (iii) follows from the multiplicity one property of generic representations. In Section 4, we present another useful application of the above approach to proving that an
$\mathcal {A}$
-module (see [Reference Chan and Savin11, Lemmas 2.2 and 2.3]). The Gelfand–Graev representation can be shown to satisfy properties (i)–(iii): Property (i) is provided by Corollary 8.6 of [Reference Chan and Savin11]; (ii) is proved in [Reference Bushnell and Henniart6], and (iii) follows from the multiplicity one property of generic representations. In Section 4, we present another useful application of the above approach to proving that an
![]() $\mathcal {H}$
-module is isomorphic to
$\mathcal {H}$
-module is isomorphic to
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
Proposition 3.1 suggests the following approach to determine the
![]() $\mathcal {H}$
-module structure of
$\mathcal {H}$
-module structure of
![]() $\Pi $
: First, we find all possible
$\Pi $
: First, we find all possible
![]() $\mathcal {H}$
-module structures on
$\mathcal {H}$
-module structures on
![]() $\mathcal {A}$
. After that, we need to only determine which one of those structures describes
$\mathcal {A}$
. After that, we need to only determine which one of those structures describes
![]() $\Pi $
. In the following subsection, we compute the possible
$\Pi $
. In the following subsection, we compute the possible
![]() $\mathcal {H}$
-structures on
$\mathcal {H}$
-structures on
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
3.1
 $\mathcal {H}$
-module structures on
$\mathcal {H}$
-module structures on
 $\mathcal {A}$
$\mathcal {A}$
In order to treat the case of general Bernstein components—and not just those described in Section 2.6—we work in a slightly more general setting in this section. We thus investigate the possible
![]() $\mathcal {H}$
-module structures on
$\mathcal {H}$
-module structures on
![]() $\mathcal {A}$
(where
$\mathcal {A}$
(where
![]() $\mathcal {H}$
is generated by
$\mathcal {H}$
is generated by
![]() $T_0,\dotsc , T_n$
over
$T_0,\dotsc , T_n$
over
![]() $\mathcal {A}$
), but we assume that
$\mathcal {A}$
), but we assume that
![]() $\mathcal {A} = \mathcal {A}'[X_1^{\pm },\dotsc , X_n^{\pm }]$
, where
$\mathcal {A} = \mathcal {A}'[X_1^{\pm },\dotsc , X_n^{\pm }]$
, where
![]() $\mathcal {A}'$
is an integral domain containing
$\mathcal {A}'$
is an integral domain containing
![]() $\mathbb {C}$
as a subring. For Bernstein components described in Section 2.6, we have
$\mathbb {C}$
as a subring. For Bernstein components described in Section 2.6, we have
![]() $\mathcal {A}' = \mathbb {C}$
; in general,
$\mathcal {A}' = \mathbb {C}$
; in general,
![]() $\mathcal {A}'$
itself is a (Laurent) polynomial ring over
$\mathcal {A}'$
itself is a (Laurent) polynomial ring over
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
First, assume that we are in Case (i) (see Section 2.6). Then the situation is precisely the one treated in [Reference Chan and Savin11], and the possible
![]() $\mathcal {H}$
-module structures on
$\mathcal {H}$
-module structures on
![]() $\mathcal {A}$
are determined in Section 2.2 there. We have the following.
$\mathcal {A}$
are determined in Section 2.2 there. We have the following.
Proposition 3.3 (Case (i))
Let
![]() $\Pi $
be an
$\Pi $
be an
![]() $\mathcal {H}$
-module which is isomorphic to
$\mathcal {H}$
-module which is isomorphic to
![]() $\mathcal {A}$
as an
$\mathcal {A}$
as an
![]() $\mathcal {A}$
-module. Then
$\mathcal {A}$
-module. Then
![]() $\Pi \cong \mathcal {H} \otimes _{\mathcal {H}_{S_n}} \epsilon $
, where
$\Pi \cong \mathcal {H} \otimes _{\mathcal {H}_{S_n}} \epsilon $
, where
![]() $\epsilon $
is a one-dimensional representation of
$\epsilon $
is a one-dimensional representation of
![]() $\mathcal {H}_{S_n}$
.
$\mathcal {H}_{S_n}$
.
Here,
![]() $\mathcal {H}_{S_n}$
denotes the finite-dimensional algebra generated by
$\mathcal {H}_{S_n}$
denotes the finite-dimensional algebra generated by
![]() $T_1,\dotsc ,T_{n-1}$
; we have
$T_1,\dotsc ,T_{n-1}$
; we have
![]() $\mathcal {H} = \mathcal {A} \otimes _{\mathbb {C}} \mathcal {H}_{S_n}$
. Furthermore,
$\mathcal {H} = \mathcal {A} \otimes _{\mathbb {C}} \mathcal {H}_{S_n}$
. Furthermore,
![]() $\mathcal {H}_{S_n}$
has precisely two one-dimensional representations:
$\mathcal {H}_{S_n}$
has precisely two one-dimensional representations:
 $$ \begin{align*} \epsilon_{-1}: T_i \mapsto -1 \quad &\text{ for } i = 1, \dotsc, n-1; \quad \text{and}\\ \epsilon_{q^t}: T_i \mapsto q^t \quad &\text{ for } i = 1, \dotsc, n-1. \end{align*} $$
$$ \begin{align*} \epsilon_{-1}: T_i \mapsto -1 \quad &\text{ for } i = 1, \dotsc, n-1; \quad \text{and}\\ \epsilon_{q^t}: T_i \mapsto q^t \quad &\text{ for } i = 1, \dotsc, n-1. \end{align*} $$
We now treat Cases (ii) and (iii) simultaneously. Recall that, in these cases, the algebra
![]() $\mathcal {H}$
is described by an affine Coxeter diagram of type
$\mathcal {H}$
is described by an affine Coxeter diagram of type
![]() $\tilde {C}_n$
. We let
$\tilde {C}_n$
. We let
![]() $\mathcal {H}_0$
and
$\mathcal {H}_0$
and
![]() $\mathcal {H}_n$
denote the algebras obtained by removing the vertices which correspond to
$\mathcal {H}_n$
denote the algebras obtained by removing the vertices which correspond to
![]() $T_0$
and
$T_0$
and
![]() $T_n$
, respectively. In other words,
$T_n$
, respectively. In other words,
![]() $\mathcal {H}_0$
is generated by
$\mathcal {H}_0$
is generated by
![]() $T_1,\dotsc ,T_n$
as an
$T_1,\dotsc ,T_n$
as an
![]() $\mathcal {A}$
-algebra, whereas
$\mathcal {A}$
-algebra, whereas
![]() $\mathcal {H}_n$
is generated by
$\mathcal {H}_n$
is generated by
![]() $T_0,\dotsc ,T_{n-1}$
. Note that we have
$T_0,\dotsc ,T_{n-1}$
. Note that we have
![]() $\mathcal {H} = \mathcal {A} \otimes _{\mathbb {C}}\mathcal {H}_n = \mathcal {A} \otimes _{\mathbb {C}}\mathcal {H}_0$
. We now prove the following result.
$\mathcal {H} = \mathcal {A} \otimes _{\mathbb {C}}\mathcal {H}_n = \mathcal {A} \otimes _{\mathbb {C}}\mathcal {H}_0$
. We now prove the following result.
Proposition 3.4 (Cases (ii) and (iii))
Let
![]() $\Pi $
be an
$\Pi $
be an
![]() $\mathcal {H}$
-module which is isomorphic to
$\mathcal {H}$
-module which is isomorphic to
![]() $\mathcal {A}$
as an
$\mathcal {A}$
as an
![]() $\mathcal {A}$
-module. Then
$\mathcal {A}$
-module. Then
Here,
![]() $\epsilon _0$
(resp.
$\epsilon _0$
(resp.
![]() $\epsilon _n$
) is a one-dimensional representation of
$\epsilon _n$
) is a one-dimensional representation of
![]() $\mathcal {H}_{0}$
(resp.
$\mathcal {H}_{0}$
(resp.
![]() $\mathcal {H}_{n}$
).
$\mathcal {H}_{n}$
).
Proof We first restrict our attention to the subalgebra generated by
![]() $T_1,\dotsc , T_{n-1}$
, which is contained in both
$T_1,\dotsc , T_{n-1}$
, which is contained in both
![]() $\mathcal {H}_0$
and
$\mathcal {H}_0$
and
![]() $\mathcal {H}_n$
. This is precisely the algebra
$\mathcal {H}_n$
. This is precisely the algebra
![]() $\mathcal {H}_{S_n}$
discussed in [Reference Chan and Savin11]. The possible
$\mathcal {H}_{S_n}$
discussed in [Reference Chan and Savin11]. The possible
![]() $\mathcal {H}_{S_n}$
-structures on
$\mathcal {H}_{S_n}$
-structures on
![]() $\mathcal {A}$
are determined in Section 2.2 there. To summarize the relevant results, there exists an invertible element
$\mathcal {A}$
are determined in Section 2.2 there. To summarize the relevant results, there exists an invertible element
![]() $g_0\in \mathcal {A}$
on which the operators
$g_0\in \mathcal {A}$
on which the operators
![]() $T_1,\dots ,T_n$
act by the same scalar, either
$T_1,\dots ,T_n$
act by the same scalar, either
![]() $q^t$
or
$q^t$
or
![]() $-1$
.
$-1$
.
We now determine how
![]() $T_0$
and
$T_0$
and
![]() $T_n$
act on
$T_n$
act on
![]() $g_0$
. Since
$g_0$
. Since
![]() $g_0$
is invertible, we have
$g_0$
is invertible, we have
![]() $T_ng_0 = fg_0$
for some
$T_ng_0 = fg_0$
for some
![]() $f\in \mathcal {A}$
. Recall that
$f\in \mathcal {A}$
. Recall that
![]() $T_n$
satisfies the quadratic relation
$T_n$
satisfies the quadratic relation
as well as the commutation relation
 $$\begin{align*}T_nf- f^{\vee} T_n = \left((q^r-1) + \frac{1}{X_n}(\sqrt{q}^{r+s}-\sqrt{q}^{r-s})\right)\frac{f-f^{\vee}}{1-1/X_n^2}. \end{align*}$$
$$\begin{align*}T_nf- f^{\vee} T_n = \left((q^r-1) + \frac{1}{X_n}(\sqrt{q}^{r+s}-\sqrt{q}^{r-s})\right)\frac{f-f^{\vee}}{1-1/X_n^2}. \end{align*}$$
Here, and throughout the proof, we let
![]() $r=s=0$
if we are considering Case (ii). Recall that
$r=s=0$
if we are considering Case (ii). Recall that
![]() $f^{\vee }$
denotes the function
$f^{\vee }$
denotes the function
![]() $f^{\vee }(X_1,\dotsc ,X_n) = f(X_1,\dotsc ,X_{n-1},\frac {1}{X_n})$
. Using the above and comparing the two sides of
$f^{\vee }(X_1,\dotsc ,X_n) = f(X_1,\dotsc ,X_{n-1},\frac {1}{X_n})$
. Using the above and comparing the two sides of
![]() $T_n^2g_0 = (q^r-1)T_ng_0 + q^rg_0$
, we get
$T_n^2g_0 = (q^r-1)T_ng_0 + q^rg_0$
, we get
 $$\begin{align*}ff^{\vee} = (q^r-1)\frac{X_nf^{\vee}-\frac{1}{X_n}f}{X_n-\frac{1}{X_n}} - (\sqrt{q}^{r+s}-\sqrt{q}^{r-s})\frac{f-f^{\vee}}{X_n-\frac{1}{X_n}} + q^r. \end{align*}$$
$$\begin{align*}ff^{\vee} = (q^r-1)\frac{X_nf^{\vee}-\frac{1}{X_n}f}{X_n-\frac{1}{X_n}} - (\sqrt{q}^{r+s}-\sqrt{q}^{r-s})\frac{f-f^{\vee}}{X_n-\frac{1}{X_n}} + q^r. \end{align*}$$
To simplify notation, we now set
![]() $b = q^r-1$
and
$b = q^r-1$
and
![]() $c = (\sqrt {q}^{r+s}-\sqrt {q}^{r-s})$
. We also temporarily drop the index n, writing X instead of
$c = (\sqrt {q}^{r+s}-\sqrt {q}^{r-s})$
. We also temporarily drop the index n, writing X instead of
![]() $X_n$
. Clearing out the denominators, we rearrange the above equation into
$X_n$
. Clearing out the denominators, we rearrange the above equation into
Our first goal is to find the possible solutions
![]() $f\in \mathcal {A}$
of this equation.
$f\in \mathcal {A}$
of this equation.
Lemma 3.5 The above equation has the following solutions:
along with the constant solutions
![]() $f = q^t$
and
$f = q^t$
and
![]() $f=-1$
.
$f=-1$
.
Proof Each
![]() $f\in \mathcal {A}$
can be written as
$f\in \mathcal {A}$
can be written as
for some functions
![]() $a_{-l},\dotsc ,a_k \in \mathcal {A'}[X_1^{\pm }, \dotsc , X_{n-1}^{\pm }]$
, with
$a_{-l},\dotsc ,a_k \in \mathcal {A'}[X_1^{\pm }, \dotsc , X_{n-1}^{\pm }]$
, with
![]() $a_k, a_{-l}\neq 0$
. We write
$a_k, a_{-l}\neq 0$
. We write
![]() $\text {maxdeg}(f)$
for k and
$\text {maxdeg}(f)$
for k and
![]() $\text {mindeg}(f)$
for
$\text {mindeg}(f)$
for
![]() $-l$
. Now, let f be a solution of (*). We begin our analysis of (*) by solving some special cases. We claim the following:
$-l$
. Now, let f be a solution of (*). We begin our analysis of (*) by solving some special cases. We claim the following:
 $$ \begin{align} \quad \begin{matrix} \text{If} & f =a_0, &\text{then} & a_0 = q^r \text{ or } a_0 = -1.\\ \text{If} & f =a_1X, &\text{then} & a_1 = \mp\sqrt{q}^{r\pm s}.\\ \text{If} & f = a_0 + a_{-1}X^{-1} \text{ and } a_{-1}\neq 0, &\text{ then } & a_0 = b \text{ and } a_{-1} = \pm\sqrt{q}^{r\pm s}. \end{matrix} \end{align} $$
$$ \begin{align} \quad \begin{matrix} \text{If} & f =a_0, &\text{then} & a_0 = q^r \text{ or } a_0 = -1.\\ \text{If} & f =a_1X, &\text{then} & a_1 = \mp\sqrt{q}^{r\pm s}.\\ \text{If} & f = a_0 + a_{-1}X^{-1} \text{ and } a_{-1}\neq 0, &\text{ then } & a_0 = b \text{ and } a_{-1} = \pm\sqrt{q}^{r\pm s}. \end{matrix} \end{align} $$
To verify this, we first look at solutions
![]() $f = a_0$
. In this case, the equation (*) reduces to
$f = a_0$
. In this case, the equation (*) reduces to
![]() $a_0^2 = ba_0 + q^r$
. This equation has two constant solutions,
$a_0^2 = ba_0 + q^r$
. This equation has two constant solutions,
![]() $a_0 = -1$
and
$a_0 = -1$
and
![]() $a_0 = q^r$
. These are also the only solutions, since
$a_0 = q^r$
. These are also the only solutions, since
![]() $\mathcal {A}$
has no zero divisors. When
$\mathcal {A}$
has no zero divisors. When
![]() $f(X) = a_1X$
, the equation becomes
$f(X) = a_1X$
, the equation becomes
![]() $a_1^2 + a_1c - q^r = 0$
. Again, the only two solutions of this equation are the constant ones:
$a_1^2 + a_1c - q^r = 0$
. Again, the only two solutions of this equation are the constant ones:
![]() $a_1 = \mp \sqrt {q}^{r\pm s}$
. Finally, when
$a_1 = \mp \sqrt {q}^{r\pm s}$
. Finally, when
![]() $f = a_0 +a_{-1}X^{-1}$
, the equation reduces to the following system:
$f = a_0 +a_{-1}X^{-1}$
, the equation reduces to the following system:
Since we are assuming that
![]() $a_1\neq 0$
, the first equation gives us
$a_1\neq 0$
, the first equation gives us
![]() $a_0 = b$
, and then the second becomes
$a_0 = b$
, and then the second becomes
![]() $a_{-1}^2 - ca_{-1} - q^r = 0$
. Again, we have two solutions:
$a_{-1}^2 - ca_{-1} - q^r = 0$
. Again, we have two solutions:
![]() $a_{-1} = \pm \sqrt {q}^{r\pm s}$
.
$a_{-1} = \pm \sqrt {q}^{r\pm s}$
.
Next, when f is a solution of (*) given by (†), we observe
Indeed, let LHS and RHS denote the left-hand side and the right-hand side of (*), respectively. We then have
![]() $\mathrm{maxdeg(LHS)} = k+l+2$
, whereas
$\mathrm{maxdeg(LHS)} = k+l+2$
, whereas
![]() $\mathrm{maxdeg(RHS)} \leq \max \{l+2,k+1,2\}$
. Therefore, equality of degrees cannot be achieved unless
$\mathrm{maxdeg(RHS)} \leq \max \{l+2,k+1,2\}$
. Therefore, equality of degrees cannot be achieved unless
![]() $k \leq 0$
or
$k \leq 0$
or
![]() $l\leq 0$
. In fact, the same argument gives us a slightly stronger statement in one case:
$l\leq 0$
. In fact, the same argument gives us a slightly stronger statement in one case:
Finally, we make use of the following fact, which is readily verified by direct computation:
 $$ \begin{align} \begin{aligned} &\text{For any positive integer } d, f \text{ is a solution of (*) if and only if }\\ &\qquad\qquad\qquad\qquad X^{2d}f-R_d \text{ is also a solution.} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\text{For any positive integer } d, f \text{ is a solution of (*) if and only if }\\ &\qquad\qquad\qquad\qquad X^{2d}f-R_d \text{ is also a solution.} \end{aligned} \end{align} $$
Here,
![]() $R_d = \dfrac {bX^2+cX}{X^2-1}(X^{2d}-1) = bX^{2d} + cX^{2d-1}+\cdots +bX^2+cX$
.
$R_d = \dfrac {bX^2+cX}{X^2-1}(X^{2d}-1) = bX^{2d} + cX^{2d-1}+\cdots +bX^2+cX$
.
We are now ready to find all the solutions. By (3.2), any solution of f contains either only positive powers of X, or only nonpositive. We therefore consider two separate cases.
Case A: f has only nonpositive powers, i.e.,
![]() $f = a_0 + a_{-1}X^{-1} + \dotsb + a_{-l}X^{-l}$
.
$f = a_0 + a_{-1}X^{-1} + \dotsb + a_{-l}X^{-l}$
.
Let
![]() $d = \lfloor l/2 \rfloor $
. We use (3.4) and look at another solution,
$d = \lfloor l/2 \rfloor $
. We use (3.4) and look at another solution,
![]() $g = X^{2d}f - R_d$
.
$g = X^{2d}f - R_d$
.
We first assume that
![]() $l=2d$
is even. In this case, g only has nonnegative powers of X, but it has a nonzero constant term,
$l=2d$
is even. In this case, g only has nonnegative powers of X, but it has a nonzero constant term,
![]() $a_{-l}$
. Therefore, (3.3) shows that the coefficients next to the positive powers must be zero:
$a_{-l}$
. Therefore, (3.3) shows that the coefficients next to the positive powers must be zero:
![]() $a_0-b = a_{-1}-c= \dotsb = a_{-l+1}-c = 0$
. Now, (3.1) shows that there are only two possibilities for the constant term:
$a_0-b = a_{-1}-c= \dotsb = a_{-l+1}-c = 0$
. Now, (3.1) shows that there are only two possibilities for the constant term:
![]() $a_{-l} = q^t$
or
$a_{-l} = q^t$
or
![]() $a_{-l} = -1$
. We thus get two solutions:
$a_{-l} = -1$
. We thus get two solutions:
 $$\begin{align*}&f = b + cX^{-1} + bX^{-2} + \cdots + cX^{1-2d} +q^tX^{-2d} \text{ } \text{ and } \\ & f = b + cX^{-1} + bX^{-2} + \cdots + cX^{1-2d} - X^{-2d}. \end{align*}$$
$$\begin{align*}&f = b + cX^{-1} + bX^{-2} + \cdots + cX^{1-2d} +q^tX^{-2d} \text{ } \text{ and } \\ & f = b + cX^{-1} + bX^{-2} + \cdots + cX^{1-2d} - X^{-2d}. \end{align*}$$
Next, assume that
![]() $l=2d+1$
is odd. Now, g has a nonzero coefficient (i.e.,
$l=2d+1$
is odd. Now, g has a nonzero coefficient (i.e.,
![]() $a_{-l}$
) next to
$a_{-l}$
) next to
![]() $X^{-1}$
, so by (3.2) the coefficients next to positive powers must be equal to
$X^{-1}$
, so by (3.2) the coefficients next to positive powers must be equal to
![]() $0$
. This gives us
$0$
. This gives us
![]() $a_0 = b, a_{-1} = c, \dotsc , a_{2-l} = c$
. Furthermore, g is thus of the form
$a_0 = b, a_{-1} = c, \dotsc , a_{2-l} = c$
. Furthermore, g is thus of the form
![]() $a_{1-l} + a_{-l}X^{-1}$
, so we can read off the coefficients
$a_{1-l} + a_{-l}X^{-1}$
, so we can read off the coefficients
![]() $a_{1-l}$
and
$a_{1-l}$
and
![]() $a_{-l}$
from (3.1). We thus arrive at two more solutions:
$a_{-l}$
from (3.1). We thus arrive at two more solutions:
Case B: f only has positive powers, i.e.,
![]() $f = a_kX^k +\cdots + a_1X$
.
$f = a_kX^k +\cdots + a_1X$
.
This time, we set
![]() $d = \lfloor k/2 \rfloor $
and use (3.4) to obtain the solution
$d = \lfloor k/2 \rfloor $
and use (3.4) to obtain the solution
![]() $g = \dfrac {1}{X^{2d}}(f+R_d)$
.
$g = \dfrac {1}{X^{2d}}(f+R_d)$
.
First, assume that
![]() $k = 2d+1$
is odd. Then g has a nonzero coefficient (i.e.,
$k = 2d+1$
is odd. Then g has a nonzero coefficient (i.e.,
![]() $a_k$
) next to X, so (3.2) and (3.3) imply that all the lower coefficients are zero. This immediately gives us
$a_k$
) next to X, so (3.2) and (3.3) imply that all the lower coefficients are zero. This immediately gives us
![]() $a_1 = -c, a_2 = -b, \dotsc , a_{2d} = -b$
. Furthermore, we have
$a_1 = -c, a_2 = -b, \dotsc , a_{2d} = -b$
. Furthermore, we have
![]() $g = a_kX$
, so (3.1) shows that we have two possibilities for
$g = a_kX$
, so (3.1) shows that we have two possibilities for
![]() $a_k$
. We therefore get two solutions:
$a_k$
. We therefore get two solutions:
Finally, assume that
![]() $k=2d$
is even. First, if
$k=2d$
is even. First, if
![]() $k> 2$
, consider another solution
$k> 2$
, consider another solution
![]() $g' = X^{2-2d}(f+R_{2d-2})$
. Now,
$g' = X^{2-2d}(f+R_{2d-2})$
. Now,
![]() $g'$
has a nonzero coefficient (i.e.,
$g'$
has a nonzero coefficient (i.e.,
![]() $a_k$
) next to
$a_k$
) next to
![]() $X^2$
, so the coefficient next to nonpositive powers of X have to be
$X^2$
, so the coefficient next to nonpositive powers of X have to be
![]() $0$
by (3.2) and (3.3). This gives us
$0$
by (3.2) and (3.3). This gives us
![]() $a_1 = -c, a_2 = -b, \dotsc , a_{2d-2}= -b$
. In particular, this shows that
$a_1 = -c, a_2 = -b, \dotsc , a_{2d-2}= -b$
. In particular, this shows that
![]() $g = (a_k+b) + (a_{k-1}+c)X^{-1}$
. Since
$g = (a_k+b) + (a_{k-1}+c)X^{-1}$
. Since
![]() $a_k + b \neq b$
(i.e.,
$a_k + b \neq b$
(i.e.,
![]() $a_k\neq 0$
), (3.1) shows that we have only two possibilities:
$a_k\neq 0$
), (3.1) shows that we have only two possibilities:
In other words,
![]() $a_{k-1} = -c$
and
$a_{k-1} = -c$
and
![]() $a_k \in \{-q^r, 1\}$
. We thus get the remaining solutions:
$a_k \in \{-q^r, 1\}$
. We thus get the remaining solutions:
We continue the proof of Proposition 3.4. We have just proved that
![]() $T_ng_0 = fg_0$
where
$T_ng_0 = fg_0$
where
![]() $f\in \mathcal {A}$
is one of the elements listed in Lemma 3.5. First, assume that f is one of the constant solutions, i.e.,
$f\in \mathcal {A}$
is one of the elements listed in Lemma 3.5. First, assume that f is one of the constant solutions, i.e.,
![]() $f=-1$
or
$f=-1$
or
![]() $f=q^r$
. Then
$f=q^r$
. Then
![]() $g_0$
is an invertible element of
$g_0$
is an invertible element of
![]() $\mathcal {A}$
on which
$\mathcal {A}$
on which
![]() $T_1, \dotsc , T_{n-1}, T_n$
all act as scalars. In other words, we have a one-dimensional representation
$T_1, \dotsc , T_{n-1}, T_n$
all act as scalars. In other words, we have a one-dimensional representation
![]() $\epsilon _0$
of the algebra
$\epsilon _0$
of the algebra
![]() $\mathcal {H}_0$
. Since
$\mathcal {H}_0$
. Since
![]() $\mathcal {H} = \mathcal {A} \otimes _{\mathbb {C}} \mathcal {H}_0$
, it follows that the corresponding
$\mathcal {H} = \mathcal {A} \otimes _{\mathbb {C}} \mathcal {H}_0$
, it follows that the corresponding
![]() $\mathcal {H}$
-module structure on
$\mathcal {H}$
-module structure on
![]() $\mathcal {A}$
is isomorphic to
$\mathcal {A}$
is isomorphic to
Now, if f is of type (i) or (ii) listed in the statement of Lemma 3.5, set
Since
![]() $(X_1X_2\cdot \dotsb \cdot X_n)^{-d}$
commutes with
$(X_1X_2\cdot \dotsb \cdot X_n)^{-d}$
commutes with
![]() $T_1,\dotsc ,T_{n-1}$
,
$T_1,\dotsc ,T_{n-1}$
,
![]() $g_1$
is still an eigenvector for each of these operators. We claim that
$g_1$
is still an eigenvector for each of these operators. We claim that
![]() $g_1$
is an eigenvector for
$g_1$
is an eigenvector for
![]() $T_n$
as well. Indeed, using the appropriate commutation relation and the fact that
$T_n$
as well. Indeed, using the appropriate commutation relation and the fact that
![]() $T_n$
commutes with
$T_n$
commutes with
![]() $X_1, \dotsc , X_{n-1}$
, we get
$X_1, \dotsc , X_{n-1}$
, we get
 $$ \begin{align*} T_ng_1 &= (X_1X_2\cdot \dotsb \cdot X_{n-1})^{-d}\cdot T_nX_n^{-d}g_0\\ &= (X_1X_2\cdot \dotsb \cdot X_{n-1})^{-d}\left(X_n^dT_n + \frac{bX_n+c}{X_n^2-1}(X_n^{-d}-X_n^d)\right)g_0\\ &= (X_1X_2\cdot \dotsb \cdot X_{n-1})^{-d}\left(X_n^df + \frac{bX_n+c}{X_n^2-1}(X_n^{-d}-X_n^d)\right)g_0\\ &= (X_1X_2\cdot \dotsb \cdot X_{n-1})^{-d}\left(X_n^{2d}f - \frac{bX_n+c}{X_n^2-1}(X_n^{2d}-1)\right)g_0. \end{align*} $$
$$ \begin{align*} T_ng_1 &= (X_1X_2\cdot \dotsb \cdot X_{n-1})^{-d}\cdot T_nX_n^{-d}g_0\\ &= (X_1X_2\cdot \dotsb \cdot X_{n-1})^{-d}\left(X_n^dT_n + \frac{bX_n+c}{X_n^2-1}(X_n^{-d}-X_n^d)\right)g_0\\ &= (X_1X_2\cdot \dotsb \cdot X_{n-1})^{-d}\left(X_n^df + \frac{bX_n+c}{X_n^2-1}(X_n^{-d}-X_n^d)\right)g_0\\ &= (X_1X_2\cdot \dotsb \cdot X_{n-1})^{-d}\left(X_n^{2d}f - \frac{bX_n+c}{X_n^2-1}(X_n^{2d}-1)\right)g_0. \end{align*} $$
Simplifying the expression in the parentheses, we obtain
![]() $\lambda X_n^{-d}$
, so that
$\lambda X_n^{-d}$
, so that
![]() $T_ng_1 = \lambda g_1$
, where
$T_ng_1 = \lambda g_1$
, where
![]() $\lambda = q^t$
(resp.
$\lambda = q^t$
(resp.
![]() $-1$
) when f is of type (i) (resp. (ii)). We have thus once more found a common eigenvector for
$-1$
) when f is of type (i) (resp. (ii)). We have thus once more found a common eigenvector for
![]() $T_1,\dotsc ,T_{n-1},T_n$
. Again, we deduce that the corresponding
$T_1,\dotsc ,T_{n-1},T_n$
. Again, we deduce that the corresponding
![]() $\mathcal {H}$
-module structure is isomorphic to
$\mathcal {H}$
-module structure is isomorphic to
![]() $\mathcal {H}\otimes _{ \mathcal {H}_0} \epsilon _0$
, where
$\mathcal {H}\otimes _{ \mathcal {H}_0} \epsilon _0$
, where
![]() $\epsilon _0$
is a one-dimensional representation of
$\epsilon _0$
is a one-dimensional representation of
![]() $\mathcal {H}_0$
.
$\mathcal {H}_0$
.
When f is of type (v) or (vi), we use the same argument and arrive at the same conclusion. The only difference in this case is that we have to set
![]() $g_1 = (X_1X_2\cdot \dotsb \cdot X_n)^{d}g_0$
in order to obtain a common eigenvector for
$g_1 = (X_1X_2\cdot \dotsb \cdot X_n)^{d}g_0$
in order to obtain a common eigenvector for
![]() $T_1,\dotsc ,T_{n-1},T_n$
.
$T_1,\dotsc ,T_{n-1},T_n$
.
In the remaining cases—that is, when f is of type (iii) or (iv)—we cannot find such an eigenvector, but we claim that we can find an invertible
![]() $g_1 \in A$
which is a common eigenvector for
$g_1 \in A$
which is a common eigenvector for
![]() $T_0, T_1, \dotsc , T_{n-1}$
. Just like in the previous cases, this will imply that the
$T_0, T_1, \dotsc , T_{n-1}$
. Just like in the previous cases, this will imply that the
![]() $\mathcal {H}$
-structure on
$\mathcal {H}$
-structure on
![]() $\mathcal {A}$
is isomorphic to
$\mathcal {A}$
is isomorphic to
![]() $\mathcal {H}\otimes _{ \mathcal {H}_n} \epsilon _n$
for some one-dimensional representation
$\mathcal {H}\otimes _{ \mathcal {H}_n} \epsilon _n$
for some one-dimensional representation
![]() $\epsilon _n$
of
$\epsilon _n$
of
![]() $\mathcal {H}_n$
.
$\mathcal {H}_n$
.
If
![]() $T_ng_0 = fg_0$
with f of type (iii), we set
$T_ng_0 = fg_0$
with f of type (iii), we set
![]() $g_1 = (X_1X_2\cdot \dotsb \cdot X_n)^{-d}g_0$
. If f is of type (iv), let
$g_1 = (X_1X_2\cdot \dotsb \cdot X_n)^{-d}g_0$
. If f is of type (iv), let
![]() $g_1 = (X_1X_2\cdot \dotsb \cdot X_n)^{d+1}g_0$
. In both cases,
$g_1 = (X_1X_2\cdot \dotsb \cdot X_n)^{d+1}g_0$
. In both cases,
![]() $g_1$
is an eigenvector for
$g_1$
is an eigenvector for
![]() $T_1,\dotsc , T_{n-1}$
and a computation analogous to the one we carried out in for Cases (i) and (ii) shows that we have
$T_1,\dotsc , T_{n-1}$
and a computation analogous to the one we carried out in for Cases (i) and (ii) shows that we have
The following lemma then shows that
![]() $g_1$
is also an eigenvector for
$g_1$
is also an eigenvector for
![]() $T_0$
and thus concludes the proof of Proposition 3.4.
$T_0$
and thus concludes the proof of Proposition 3.4.
Lemma 3.6 Let g be an invertible element of
![]() $\mathcal {A}$
, which is an eigenvector for
$\mathcal {A}$
, which is an eigenvector for
![]() $T_1, \dotsc , T_{n-1}$
, such that
$T_1, \dotsc , T_{n-1}$
, such that
![]() $T_ng = (b\pm \sqrt {q}^{r\pm s}X_n^{-1})g$
. Then g is also an eigenvector for
$T_ng = (b\pm \sqrt {q}^{r\pm s}X_n^{-1})g$
. Then g is also an eigenvector for
![]() $T_0$
.
$T_0$
.
Proof Recall that
![]() $T_0 = \sqrt {q}^{s+2(n-1)t+r}X_1T_w^{-1}$
, with
$T_0 = \sqrt {q}^{s+2(n-1)t+r}X_1T_w^{-1}$
, with
![]() $T_w = T_1\dotsm T_{n-1}T_nT_{n-1}\dotsm T_1$
. In both cases, all the operators
$T_w = T_1\dotsm T_{n-1}T_nT_{n-1}\dotsm T_1$
. In both cases, all the operators
![]() $T_1,\dotsc ,T_{n-1}$
act by the same scalar
$T_1,\dotsc ,T_{n-1}$
act by the same scalar
![]() $\lambda \in \{-1,q^t\}$
. We therefore have
$\lambda \in \{-1,q^t\}$
. We therefore have
We now recall that
![]() $T_n^{-1} = \frac {1}{q^r}(T_n-b)$
; this follows from the quadratic relation for
$T_n^{-1} = \frac {1}{q^r}(T_n-b)$
; this follows from the quadratic relation for
![]() $T_n$
. Therefore, by the assumption in the statement of the lemma,
$T_n$
. Therefore, by the assumption in the statement of the lemma,
![]() $T_n^{-1}g = \pm \sqrt {q}^{\pm s -r}X_n^{-1}$
. Thus,
$T_n^{-1}g = \pm \sqrt {q}^{\pm s -r}X_n^{-1}$
. Thus,
with
![]() $\mu \in \{-1, q^s\}$
. Finally, it remains to notice that, for every
$\mu \in \{-1, q^s\}$
. Finally, it remains to notice that, for every
![]() $i = 1, \dotsc , n-1$
, we have
$i = 1, \dotsc , n-1$
, we have
Indeed, from the quadratic relation, we have
![]() $T_i^{-1}= \frac {1}{q^t}(T_i - (q^t-1))$
. Combining this with the commutation relation for
$T_i^{-1}= \frac {1}{q^t}(T_i - (q^t-1))$
. Combining this with the commutation relation for
![]() $T_i$
, we get (3.6). Successively applying (3.6) to (3.5) (and taking into account that each
$T_i$
, we get (3.6). Successively applying (3.6) to (3.5) (and taking into account that each
![]() $T_i$
acts on g by
$T_i$
acts on g by
![]() $\lambda $
), we get
$\lambda $
), we get
which we needed to prove. Notice that the possible eigenvalues are precisely the zeros of
![]() $(x-q^s)(x+1) = 0$
, the quadratic equation satisfied by
$(x-q^s)(x+1) = 0$
, the quadratic equation satisfied by
![]() $T_0$
.
$T_0$
.
The above lemma shows that, in Cases (iii) and (iv), we have an invertible element
![]() $g_1 \in \mathcal {A}$
which is a common eigenvector for
$g_1 \in \mathcal {A}$
which is a common eigenvector for
![]() $T_0,T_1,\dotsc , T_n$
. Consequently, the
$T_0,T_1,\dotsc , T_n$
. Consequently, the
![]() $\mathcal {H}$
-module structure on
$\mathcal {H}$
-module structure on
![]() $\mathcal {A}$
is given by
$\mathcal {A}$
is given by
![]() $\mathcal {H}\otimes _{ \mathcal {H}_n} \epsilon _n$
for some one-dimensional representation
$\mathcal {H}\otimes _{ \mathcal {H}_n} \epsilon _n$
for some one-dimensional representation
![]() $\epsilon _n$
of
$\epsilon _n$
of
![]() $\mathcal {H}_n$
. This concludes the proof of Proposition 3.4.
$\mathcal {H}_n$
. This concludes the proof of Proposition 3.4.
In view of Proposition 3.4, there are eight candidates for the
![]() $\mathcal {H}$
-structure (four, if
$\mathcal {H}$
-structure (four, if
![]() $n=1$
): First, we may take the tensor product over
$n=1$
): First, we may take the tensor product over
![]() $\mathcal {H}_0$
or
$\mathcal {H}_0$
or
![]() $\mathcal {H}_n$
; after that, there are four one-dimensional representations of
$\mathcal {H}_n$
; after that, there are four one-dimensional representations of
![]() $\mathcal {H}_0$
(resp.
$\mathcal {H}_0$
(resp.
![]() $\mathcal {H}_n$
) to choose from. To verify this, note that the braid relations imply that—in any one-dimensional representation—the operators
$\mathcal {H}_n$
) to choose from. To verify this, note that the braid relations imply that—in any one-dimensional representation—the operators
![]() $T_1, \dotsc , T_{n-1}$
act by the same scalar, which has to be a zero of the quadratic relation satisfied by
$T_1, \dotsc , T_{n-1}$
act by the same scalar, which has to be a zero of the quadratic relation satisfied by
![]() $T_i$
:
$T_i$
:
![]() $ (x-q^t)(x+1) = 0$
. We therefore have two possibilities for the action of the operators
$ (x-q^t)(x+1) = 0$
. We therefore have two possibilities for the action of the operators
![]() $T_i$
, and two additional possibilities (again, the zeros of the quadratic relation) for
$T_i$
, and two additional possibilities (again, the zeros of the quadratic relation) for
![]() $T_n$
(resp.
$T_n$
(resp.
![]() $T_0$
). For example, the one-dimensional representations of
$T_0$
). For example, the one-dimensional representations of
![]() $\mathcal {H}_0$
are given by
$\mathcal {H}_0$
are given by
 $$ \begin{align*} \epsilon_{-1,-1} &: \{T_n \mapsto -1, T_i \mapsto -1\}, \quad &\epsilon_{q^r,-1} : \{T_n \mapsto q^r, T_i \mapsto -1\},\\ \epsilon_{-1,q^t} &: \{T_n \mapsto -1, T_i \mapsto q^t\}, \quad &\epsilon_{q^r,q^t} : \{T_n \mapsto q^r, T_i \mapsto q^t\}. \end{align*} $$
$$ \begin{align*} \epsilon_{-1,-1} &: \{T_n \mapsto -1, T_i \mapsto -1\}, \quad &\epsilon_{q^r,-1} : \{T_n \mapsto q^r, T_i \mapsto -1\},\\ \epsilon_{-1,q^t} &: \{T_n \mapsto -1, T_i \mapsto q^t\}, \quad &\epsilon_{q^r,q^t} : \{T_n \mapsto q^r, T_i \mapsto q^t\}. \end{align*} $$
Corollary 3.7 General case. Let
![]() $\Pi $
be an
$\Pi $
be an
![]() $\mathcal {H}$
-module which is isomorphic to
$\mathcal {H}$
-module which is isomorphic to
![]() $\mathcal {A}$
as an
$\mathcal {A}$
as an
![]() $\mathcal {A}$
-module. Then there exists a finite subalgebra
$\mathcal {A}$
-module. Then there exists a finite subalgebra
![]() ${\mathcal H}_W \cong {\mathbb C}[W]$
, where W is a finite group, such that
${\mathcal H}_W \cong {\mathbb C}[W]$
, where W is a finite group, such that
![]() ${\mathcal H} \cong \mathcal A \otimes {\mathcal H}_W$
, and
${\mathcal H} \cong \mathcal A \otimes {\mathcal H}_W$
, and
where
![]() $\epsilon $
is a one-dimensional representation of
$\epsilon $
is a one-dimensional representation of
![]() $\mathcal {H}_{W}$
.
$\mathcal {H}_{W}$
.
Proof Recall that
![]() ${\mathcal H}$
is a tensor product of Hecke algebras each of which is isomorphic to the Iwahori Hecke algebra of
${\mathcal H}$
is a tensor product of Hecke algebras each of which is isomorphic to the Iwahori Hecke algebra of
![]() $\mathrm {GL}_n$
or an algebra of type
$\mathrm {GL}_n$
or an algebra of type
![]() $\tilde C_n$
with unequal parameters. Propositions 3.3 and 3.4 deal with these two cases, with additional flexibility that allows
$\tilde C_n$
with unequal parameters. Propositions 3.3 and 3.4 deal with these two cases, with additional flexibility that allows
![]() $\mathcal {A} = \mathcal {A}'[X_1^{\pm },\dotsc , X_n^{\pm }]$
, where
$\mathcal {A} = \mathcal {A}'[X_1^{\pm },\dotsc , X_n^{\pm }]$
, where
![]() $\mathcal {A}'={\mathbb C}[Y_1^{\pm },\dotsc , Y_m^{\pm }]$
. Thus, the corollary follows by repeated application of these two propositions.
$\mathcal {A}'={\mathbb C}[Y_1^{\pm },\dotsc , Y_m^{\pm }]$
. Thus, the corollary follows by repeated application of these two propositions.
3.2 The Gelfand–Graev module
To complete the analysis of the Gelfand–Graev representation, we need to determine which of the
![]() $\mathcal {H}$
-module structures from the previous section is isomorphic to
$\mathcal {H}$
-module structures from the previous section is isomorphic to
![]() $\Pi = ({\mathrm {c-ind}}_U^G(\psi ))_{\mathfrak {s}}$
. We consider Cases (i)–(iii) separately.
$\Pi = ({\mathrm {c-ind}}_U^G(\psi ))_{\mathfrak {s}}$
. We consider Cases (i)–(iii) separately.
Case (i). Let
![]() $\delta $
be the unique irreducible subrepresentation of
$\delta $
be the unique irreducible subrepresentation of
![]() $\rho \nu ^{\frac {n-1}{2}} \times \rho \nu ^{\frac {n-3}{2}} \times \dotsb \times \rho \nu ^{\frac {1-n}{2}}$
. Then
$\rho \nu ^{\frac {n-1}{2}} \times \rho \nu ^{\frac {n-3}{2}} \times \dotsb \times \rho \nu ^{\frac {1-n}{2}}$
. Then
![]() $\pi = \delta \rtimes \tau $
is an irreducible generic representation. The corresponding
$\pi = \delta \rtimes \tau $
is an irreducible generic representation. The corresponding
![]() $\mathcal {H}$
-module is one-dimensional: By the Bernstein version of Frobenius reciprocity, we have
$\mathcal {H}$
-module is one-dimensional: By the Bernstein version of Frobenius reciprocity, we have
 $$ \begin{align} \begin{aligned} {\mathrm{Hom}}_G(\Gamma_{\mathfrak{s}}, \pi) = {\mathrm{Hom}}_M({\mathrm{c-ind}}_{M^{\circ}}^M(\rho \otimes \dotsb \otimes \rho \otimes \tau), &\ \nu^{\frac{1-n}{2}}\rho \otimes \dotsb \otimes \nu^{\frac{n-1}{2}}\rho\otimes \tau\\ \oplus &\ \nu^{\frac{1-n}{2}}\rho^{\vee} \otimes \dotsb \otimes \nu^{\frac{n-1}{2}}\rho^{\vee} \otimes \tau). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} {\mathrm{Hom}}_G(\Gamma_{\mathfrak{s}}, \pi) = {\mathrm{Hom}}_M({\mathrm{c-ind}}_{M^{\circ}}^M(\rho \otimes \dotsb \otimes \rho \otimes \tau), &\ \nu^{\frac{1-n}{2}}\rho \otimes \dotsb \otimes \nu^{\frac{n-1}{2}}\rho\otimes \tau\\ \oplus &\ \nu^{\frac{1-n}{2}}\rho^{\vee} \otimes \dotsb \otimes \nu^{\frac{n-1}{2}}\rho^{\vee} \otimes \tau). \end{aligned} \end{align} $$
Since
![]() $\rho ^{\vee }$
is not an unramified twist of
$\rho ^{\vee }$
is not an unramified twist of
![]() $\rho $
in this case, the above
$\rho $
in this case, the above
![]() ${\mathrm {Hom}}$
-space is only one-dimensional. By Proposition 3.3,
${\mathrm {Hom}}$
-space is only one-dimensional. By Proposition 3.3,
![]() ${\mathrm {Hom}}_G(\Gamma _{\mathfrak {s}}, \Pi )$
is isomorphic to either
${\mathrm {Hom}}_G(\Gamma _{\mathfrak {s}}, \Pi )$
is isomorphic to either
![]() $\Pi \cong \mathcal {H} \otimes _{\mathcal {H}_{S_n}} \epsilon _{-1}$
or
$\Pi \cong \mathcal {H} \otimes _{\mathcal {H}_{S_n}} \epsilon _{-1}$
or
![]() $\Pi \cong \mathcal {H} \otimes _{\mathcal {H}_{S_n}} \epsilon _{q^t}$
. To determine which, we need only look at the action of
$\Pi \cong \mathcal {H} \otimes _{\mathcal {H}_{S_n}} \epsilon _{q^t}$
. To determine which, we need only look at the action of
![]() $\mathcal {H}$
on the one-dimensional module
$\mathcal {H}$
on the one-dimensional module
![]() $\pi $
. We now need to examine the definition of the operators
$\pi $
. We now need to examine the definition of the operators
![]() $T_i, i= 1,\dotsc , {n-1}$
. In [Reference Heiermann17],
$T_i, i= 1,\dotsc , {n-1}$
. In [Reference Heiermann17],
![]() $T_i$
is defined in Section 5.2 by the formula
$T_i$
is defined in Section 5.2 by the formula
 $$ \begin{align} T_i = R_i + (q^t-1)\dfrac{X_i/X_{i+1}}{X_{i}/X_{i+1}-1}. \end{align} $$
$$ \begin{align} T_i = R_i + (q^t-1)\dfrac{X_i/X_{i+1}}{X_{i}/X_{i+1}-1}. \end{align} $$
The intertwining operator
![]() $R_i$
has a pole at
$R_i$
has a pole at
![]() $0$
, and a zero at the point of reducibility (see [Reference Heiermann17, Section 1.8]). Since
$0$
, and a zero at the point of reducibility (see [Reference Heiermann17, Section 1.8]). Since
![]() $\nu ^{\frac {3-n}{2}-i}\rho \times \nu ^{\frac {3-n}{2}-i+1}\rho $
reduces, the operator
$\nu ^{\frac {3-n}{2}-i}\rho \times \nu ^{\frac {3-n}{2}-i+1}\rho $
reduces, the operator
![]() $R_i$
acts by
$R_i$
acts by
![]() $0$
in this case. It therefore remains to determine the action of
$0$
in this case. It therefore remains to determine the action of
![]() $X_i/X_{i+1}$
. Equation (3.7) shows that it suffices to determine the action of
$X_i/X_{i+1}$
. Equation (3.7) shows that it suffices to determine the action of
![]() $X_i/X_{i+1}$
on
$X_i/X_{i+1}$
on
Recalling the definition of
![]() $X_i$
(Section 2.6), we immediately see that
$X_i$
(Section 2.6), we immediately see that
![]() $X_i/X_{i+1}$
acts by
$X_i/X_{i+1}$
acts by
 $$\begin{align*}\dfrac{(|\varpi|^{\frac{3-n}{2}-i})^t}{(|\varpi|^{\frac{3-n}{2}-i+1})^t} = \frac{q^{t(\frac{n-3}{2}+i)}}{q^{t(\frac{n-3}{2}+i-1)}} = q^t. \end{align*}$$
$$\begin{align*}\dfrac{(|\varpi|^{\frac{3-n}{2}-i})^t}{(|\varpi|^{\frac{3-n}{2}-i+1})^t} = \frac{q^{t(\frac{n-3}{2}+i)}}{q^{t(\frac{n-3}{2}+i-1)}} = q^t. \end{align*}$$
This implies that
![]() $T_i$
also acts by
$T_i$
also acts by
 $(q^t-1)\dfrac {q^t}{q^t-1} = q^t$
. Since
$(q^t-1)\dfrac {q^t}{q^t-1} = q^t$
. Since
![]() $\pi $
is a quotient of
$\pi $
is a quotient of
![]() $\Pi $
, we conclude that we must have
$\Pi $
, we conclude that we must have
![]() $\Pi \cong \mathcal {H} \otimes _{\mathcal {H}_{S_n}} \epsilon _{q^t}$
.
$\Pi \cong \mathcal {H} \otimes _{\mathcal {H}_{S_n}} \epsilon _{q^t}$
.
Case (iii). In this situation, the
![]() $\mathfrak {s}$
-component of the Gelfand–Graev representation has two irreducible generic representations whose
$\mathfrak {s}$
-component of the Gelfand–Graev representation has two irreducible generic representations whose
![]() $\mathcal {H}$
-module is one-dimensional. These are the two (generalized) Steinberg representations:
$\mathcal {H}$
-module is one-dimensional. These are the two (generalized) Steinberg representations:
![]() $\pi $
and
$\pi $
and
![]() $\pi '$
, which are the unique irreducible subrepresentations of
$\pi '$
, which are the unique irreducible subrepresentations of
respectively. Recall that
![]() $\alpha $
(resp.
$\alpha $
(resp.
![]() $\beta $
) is the unique positive real number such that
$\beta $
) is the unique positive real number such that
![]() $\nu ^{\alpha }\rho \rtimes \tau $
(resp.
$\nu ^{\alpha }\rho \rtimes \tau $
(resp.
![]() $\nu ^{\beta }\rho ^{-} \rtimes \tau $
) reduces (see Section 2.6). We now compare the action of the operators
$\nu ^{\beta }\rho ^{-} \rtimes \tau $
) reduces (see Section 2.6). We now compare the action of the operators
![]() $T_0, \dotsc , T_n$
on these two representations—that is, on
$T_0, \dotsc , T_n$
on these two representations—that is, on
![]() ${\mathrm {Hom}}_G(\Gamma _{\mathfrak {s}}, \pi )$
and
${\mathrm {Hom}}_G(\Gamma _{\mathfrak {s}}, \pi )$
and
![]() ${\mathrm {Hom}}_G(\Gamma _{\mathfrak {s}}, \pi ^-)$
, where
${\mathrm {Hom}}_G(\Gamma _{\mathfrak {s}}, \pi ^-)$
, where
![]() $\Gamma _{\mathfrak {s}}$
is the projective generator defined in Section 2.4.
$\Gamma _{\mathfrak {s}}$
is the projective generator defined in Section 2.4.
We start by analyzing the action on
![]() $\pi $
. We first focus on
$\pi $
. We first focus on
![]() $T_i, i = 1, \dotsc , n-1$
. Again,
$T_i, i = 1, \dotsc , n-1$
. Again,
![]() $T_i$
is defined by (3.8), and once more, the operator
$T_i$
is defined by (3.8), and once more, the operator
![]() $R_i$
acts by
$R_i$
acts by
![]() $0$
. By the Bernstein version of Frobenius reciprocity, we have
$0$
. By the Bernstein version of Frobenius reciprocity, we have
We immediately see that
![]() $X_i/X_{i+1}$
acts by
$X_i/X_{i+1}$
acts by
 $$\begin{align*}\dfrac{(|\varpi|^{-\alpha-n+i})^t}{(|\varpi|^{-\alpha-n+i+1})^t} = \frac{q^{t(\alpha+n-i)}}{q^{t(\alpha+n-i-1)}} = q^t. \end{align*}$$
$$\begin{align*}\dfrac{(|\varpi|^{-\alpha-n+i})^t}{(|\varpi|^{-\alpha-n+i+1})^t} = \frac{q^{t(\alpha+n-i)}}{q^{t(\alpha+n-i-1)}} = q^t. \end{align*}$$
Again, this shows that
![]() $T_i$
acts by
$T_i$
acts by
 $(q^t-1)\dfrac {q^t}{q^t-1} = q^t$
. For
$(q^t-1)\dfrac {q^t}{q^t-1} = q^t$
. For
![]() $T_n$
, we have a similar formula:
$T_n$
, we have a similar formula:
 $$ \begin{align} T_n = R_n + (q^r-1)\dfrac{X_n\left(X_n-\dfrac{q^{t\beta}-q^{t\alpha}}{q^r-1}\right)}{X_n^2-1}. \end{align} $$
$$ \begin{align} T_n = R_n + (q^r-1)\dfrac{X_n\left(X_n-\dfrac{q^{t\beta}-q^{t\alpha}}{q^r-1}\right)}{X_n^2-1}. \end{align} $$
Once more,
![]() $R_n$
acts by
$R_n$
acts by
![]() $0$
, and
$0$
, and
![]() $X_n$
acts by
$X_n$
acts by
![]() $(|\varpi |^{-\alpha })^t = q^{t\alpha }$
. Recalling that
$(|\varpi |^{-\alpha })^t = q^{t\alpha }$
. Recalling that
![]() $r=t(\alpha +\beta )$
, we see that
$r=t(\alpha +\beta )$
, we see that
![]() $T_n$
acts by
$T_n$
acts by
![]() $q^r$
. Finally, since
$q^r$
. Finally, since
and since
![]() $X_1$
acts by
$X_1$
acts by
![]() $q^{(\alpha +n-1)t}$
, we see that
$q^{(\alpha +n-1)t}$
, we see that
![]() $T_0$
acts by
$T_0$
acts by
 $\dfrac {\sqrt {q}^{r+2t(n-1)+s}}{q^{2t(n-1)}\cdot q^r}q^{(\alpha +n-1)t} =q^s$
.
$\dfrac {\sqrt {q}^{r+2t(n-1)+s}}{q^{2t(n-1)}\cdot q^r}q^{(\alpha +n-1)t} =q^s$
.
We do the same with
![]() $\pi ^-$
. Again,
$\pi ^-$
. Again,
![]() $X_i/X_{i+1}$
acts by
$X_i/X_{i+1}$
acts by
![]() $q^t$
, which shows that
$q^t$
, which shows that
![]() $T_i$
acts by
$T_i$
acts by
![]() $q^t$
as well. This time
$q^t$
as well. This time
![]() $X_n$
acts by
$X_n$
acts by
![]() $-q^{t\beta }$
: Recall that
$-q^{t\beta }$
: Recall that
![]() $\rho ^{-} = \chi _0 \otimes \rho $
with
$\rho ^{-} = \chi _0 \otimes \rho $
with
![]() $X_n(\chi _0) = -1$
, so
$X_n(\chi _0) = -1$
, so
![]() $X_n(\chi _0\nu ^{-\beta })= -q^{t\beta }$
. Repeating the above calculations, we now see that
$X_n(\chi _0\nu ^{-\beta })= -q^{t\beta }$
. Repeating the above calculations, we now see that
![]() $T_n$
acts by
$T_n$
acts by
![]() $q^r$
, whereas
$q^r$
, whereas
![]() $T_0$
acts by
$T_0$
acts by
![]() $-1$
.
$-1$
.
The above analysis allows us to single out the
![]() $\mathcal {H}$
-module structure on
$\mathcal {H}$
-module structure on
![]() $\Pi $
. Since
$\Pi $
. Since
![]() $T_0$
does not act by the same scalar on
$T_0$
does not act by the same scalar on
![]() $\pi $
and
$\pi $
and
![]() $\pi ^-$
, we deduce that
$\pi ^-$
, we deduce that
![]() $\Pi = \mathcal {H} \otimes _{\mathcal {H}_0} \epsilon $
for some one-dimensional representation
$\Pi = \mathcal {H} \otimes _{\mathcal {H}_0} \epsilon $
for some one-dimensional representation
![]() $\epsilon $
of
$\epsilon $
of
![]() $\mathcal {H}_0$
. Now, since every
$\mathcal {H}_0$
. Now, since every
![]() $T_i$
(
$T_i$
(
![]() $i=1,\dotsc ,n-1$
) acts by
$i=1,\dotsc ,n-1$
) acts by
![]() $q^t$
and
$q^t$
and
![]() $T_n$
acts by
$T_n$
acts by
![]() $q^r$
, we deduce that
$q^r$
, we deduce that
![]() $\Pi = \mathcal {H} \otimes _{\mathcal {H}_0} \epsilon _{q^r,q^t}$
(see the end of Section 3.1 for notation).
$\Pi = \mathcal {H} \otimes _{\mathcal {H}_0} \epsilon _{q^r,q^t}$
(see the end of Section 3.1 for notation).
Case (ii) The first part of our analysis remains the same as in Case (iii). The representation
has two irreducible subrepresentations (both of which are in discrete series when
![]() $n>1$
, and tempered when
$n>1$
, and tempered when
![]() $n=1$
), only one of which is generic. Denote the generic subrepresentation by
$n=1$
), only one of which is generic. Denote the generic subrepresentation by
![]() $\pi $
. Let
$\pi $
. Let
![]() $\pi ^-$
denote the generic representation resulting from an analogous construction, when
$\pi ^-$
denote the generic representation resulting from an analogous construction, when
![]() $\rho $
is replaced by
$\rho $
is replaced by
![]() $\rho ^-$
. Again, the
$\rho ^-$
. Again, the
![]() $\mathcal {H}$
-modules corresponding to
$\mathcal {H}$
-modules corresponding to
![]() $\pi $
and
$\pi $
and
![]() $\pi ^-$
are one-dimensional, and the same calculations we used in Case (iii) show that the operators
$\pi ^-$
are one-dimensional, and the same calculations we used in Case (iii) show that the operators
![]() $T_i$
,
$T_i$
,
![]() $i = 1, \dotsc , n-1$
, act by
$i = 1, \dotsc , n-1$
, act by
![]() $q^t$
. This leaves us four possible
$q^t$
. This leaves us four possible
![]() $\mathcal {H}$
structures to consider
$\mathcal {H}$
structures to consider
 $$ \begin{align} \qquad \begin{aligned} \mathcal{H} \otimes_{\mathcal{H}_0} \epsilon_0, \quad \text{with} \quad &\epsilon_0(T_n) = \pm 1 \quad (\text{and }\epsilon_0(T_i) = q^t,i = 1, \dotsc, n-1); \quad \text{and}\\ \mathcal{H} \otimes_{\mathcal{H}_n} \epsilon_n, \quad \text{with} \quad &\epsilon_n(T_0) = \pm 1 \quad (\text{and }\epsilon_n(T_i) = q^t, i = 1, \dotsc, n-1). \end{aligned} \end{align} $$
$$ \begin{align} \qquad \begin{aligned} \mathcal{H} \otimes_{\mathcal{H}_0} \epsilon_0, \quad \text{with} \quad &\epsilon_0(T_n) = \pm 1 \quad (\text{and }\epsilon_0(T_i) = q^t,i = 1, \dotsc, n-1); \quad \text{and}\\ \mathcal{H} \otimes_{\mathcal{H}_n} \epsilon_n, \quad \text{with} \quad &\epsilon_n(T_0) = \pm 1 \quad (\text{and }\epsilon_n(T_i) = q^t, i = 1, \dotsc, n-1). \end{aligned} \end{align} $$
So far, we have been able to view Case (ii) as a special instance of Case (iii) which occurs when
![]() $r=s=0$
. However, to obtain an explicit description of the Gelfand–Graev module, we need more information than we used above in Case (iii). The reason is that the standard intertwining operator
$r=s=0$
. However, to obtain an explicit description of the Gelfand–Graev module, we need more information than we used above in Case (iii). The reason is that the standard intertwining operator
![]() $\chi \rho \rtimes \tau \to \chi ^{-1}\rho ^{\vee } \rtimes \tau $
no longer has a pole when
$\chi \rho \rtimes \tau \to \chi ^{-1}\rho ^{\vee } \rtimes \tau $
no longer has a pole when
![]() $X_n(\chi ) =\pm 1$
. In Case (iii), the operator
$X_n(\chi ) =\pm 1$
. In Case (iii), the operator
![]() $R_n$
(see formula (3.9))—which is constructed from the standard intertwining operator—vanishes at the point of reducibility, and the action of
$R_n$
(see formula (3.9))—which is constructed from the standard intertwining operator—vanishes at the point of reducibility, and the action of
![]() $T_n$
is determined by the action of the function
$T_n$
is determined by the action of the function
 $$\begin{align*}(q^r-1)\dfrac{X_n\left(X_n-\dfrac{q^{t\beta}-q^{t\alpha}}{q^r-1}\right)}{X_n^2-1} \end{align*}$$
$$\begin{align*}(q^r-1)\dfrac{X_n\left(X_n-\dfrac{q^{t\beta}-q^{t\alpha}}{q^r-1}\right)}{X_n^2-1} \end{align*}$$
used to remove the poles of
![]() $R_n$
. In this case, however,
$R_n$
. In this case, however,
![]() $R_n$
no longer vanishes and is regular at the point of reducibility; consequently, the above function does not appear in the construction and we have
$R_n$
no longer vanishes and is regular at the point of reducibility; consequently, the above function does not appear in the construction and we have
![]() $T_n = R_n$
. We know that this operator acts by
$T_n = R_n$
. We know that this operator acts by
![]() $1$
or
$1$
or
![]() $-1$
on the
$-1$
on the
![]() $\mathcal {H}$
-modules
$\mathcal {H}$
-modules
![]() $\pi $
and
$\pi $
and
![]() $\pi ^-$
, but we still have a certain amount of freedom in our choices. Indeed, as one verifies easily, the operator
$\pi ^-$
, but we still have a certain amount of freedom in our choices. Indeed, as one verifies easily, the operator
![]() $T_n' = (-1)^eX_n^fT_n$
(where
$T_n' = (-1)^eX_n^fT_n$
(where
![]() $e \in \{0,1\}$
and
$e \in \{0,1\}$
and
![]() $f \in \mathbb {Z}$
) satisfies the same relations as
$f \in \mathbb {Z}$
) satisfies the same relations as
![]() $T_n$
. Therefore, we obtain the same Hecke algebra if we replace
$T_n$
. Therefore, we obtain the same Hecke algebra if we replace
![]() $T_n$
by
$T_n$
by
![]() $T_n'$
, but the action of
$T_n'$
, but the action of
![]() $T_n'$
on
$T_n'$
on
![]() $\pi $
obviously differs from the action of
$\pi $
obviously differs from the action of
![]() $T_n$
.
$T_n$
.
In fact, we know that
![]() $X_n$
acts on
$X_n$
acts on
![]() $\pi $
by
$\pi $
by
![]() $1$
, and on
$1$
, and on
![]() $\pi ^-$
by
$\pi ^-$
by
![]() $-1$
. Therefore,
$-1$
. Therefore,
![]() $X_n^2$
acts by
$X_n^2$
acts by
![]() $1$
on both, so replacing
$1$
on both, so replacing
![]() $T_n$
by
$T_n$
by
![]() $X_n^2T_n$
does not affect our description of the Gelfand–Graev module. We thus have four choices that affect the description (
$X_n^2T_n$
does not affect our description of the Gelfand–Graev module. We thus have four choices that affect the description (
![]() $e = 0$
or
$e = 0$
or
![]() $1$
; f even or odd), and as we vary the four choices, the description of the Gelfand–Graev module varies through all the four possibilities described in (3.10).
$1$
; f even or odd), and as we vary the four choices, the description of the Gelfand–Graev module varies through all the four possibilities described in (3.10).
This discussion shows that—to determine the action explicitly—we need to specify the choices appearing in the construction of the operator
![]() $R_n$
. We now explain one possible normalization using Whittaker models. To be concrete, we now focus on
$R_n$
. We now explain one possible normalization using Whittaker models. To be concrete, we now focus on
![]() $G=\mathrm {SO}(2N+1)$
; the same approach is possible when G is symplectic or even orthogonal. We also specialize our discussion to the case
$G=\mathrm {SO}(2N+1)$
; the same approach is possible when G is symplectic or even orthogonal. We also specialize our discussion to the case
![]() $n=1$
to simplify notation (thus, the cuspidal representation which defines the component is
$n=1$
to simplify notation (thus, the cuspidal representation which defines the component is
![]() $\rho \otimes \tau $
); the general case is analogous and follows from this one. We thus drop the subscripts and write
$\rho \otimes \tau $
); the general case is analogous and follows from this one. We thus drop the subscripts and write
![]() $T,X$
instead of
$T,X$
instead of
![]() $T_n, X_n$
.
$T_n, X_n$
.
We fix a nondegenerate character
![]() $\psi $
of the unipotent radical U of
$\psi $
of the unipotent radical U of
![]() $G = \mathrm {SO}(2N+1)$
. Let
$G = \mathrm {SO}(2N+1)$
. Let
![]() $V_{\rho }$
denote the space of the representation
$V_{\rho }$
denote the space of the representation
![]() $\rho $
, and let
$\rho $
, and let
![]() $\lambda $
be a
$\lambda $
be a
![]() $\psi $
-Whittaker functional on
$\psi $
-Whittaker functional on
![]() $V_{\rho }$
:
$V_{\rho }$
:
![]() $\lambda (\rho (u)v) = \psi (u)\lambda (v)$
, for
$\lambda (\rho (u)v) = \psi (u)\lambda (v)$
, for
![]() $v \in V_{\rho }$
. Notice that
$v \in V_{\rho }$
. Notice that
![]() $\lambda $
is then also a
$\lambda $
is then also a
![]() $\psi $
-Whittaker functional for
$\psi $
-Whittaker functional for
![]() $\rho \otimes \chi $
for any unramified character
$\rho \otimes \chi $
for any unramified character
![]() $\chi \in \mathrm {GL}_k(F)$
: We have
$\chi \in \mathrm {GL}_k(F)$
: We have
since
![]() $\det u = 1$
and thus
$\det u = 1$
and thus
![]() $u \in \ker \chi $
. Abusing notation, we also let
$u \in \ker \chi $
. Abusing notation, we also let
![]() $\lambda $
denote the
$\lambda $
denote the
![]() $\psi $
-Whittaker functional of
$\psi $
-Whittaker functional of
![]() $\rho \otimes \tau $
(or
$\rho \otimes \tau $
(or
![]() $\chi \rho \otimes \tau $
for any unramified
$\chi \rho \otimes \tau $
for any unramified
![]() $\chi $
, as we have just shown). Following Proposition 3.1 of [Reference Shahidi24], we now form a
$\chi $
, as we have just shown). Following Proposition 3.1 of [Reference Shahidi24], we now form a
![]() $\psi $
-Whittaker functional
$\psi $
-Whittaker functional
![]() $\Lambda _{\chi }$
on the space of
$\Lambda _{\chi }$
on the space of
![]() $i_P^G(\chi \rho \otimes \tau )$
by setting
$i_P^G(\chi \rho \otimes \tau )$
by setting
where w is a representative of the nontrivial element of the Weyl group; in our case, we take w to be the block antidiagonal matrix
 $$\begin{align*}\begin{pmatrix} \mbox{ } & \mbox{ } & I_k\\ \mbox{ } & I_{2(N-k)+1} & \mbox{}\\ I_k & \mbox{ } & \mbox{} \end{pmatrix}. \end{align*}$$
$$\begin{align*}\begin{pmatrix} \mbox{ } & \mbox{ } & I_k\\ \mbox{ } & I_{2(N-k)+1} & \mbox{}\\ I_k & \mbox{ } & \mbox{} \end{pmatrix}. \end{align*}$$
Since
![]() $\pi $
and
$\pi $
and
![]() $\pi ^-$
are generic, it suffices to determine the action of T on their respective Whittaker functionals if we want to determine how T acts on the
$\pi ^-$
are generic, it suffices to determine the action of T on their respective Whittaker functionals if we want to determine how T acts on the
![]() $\mathcal {H}$
-modules
$\mathcal {H}$
-modules
![]() ${\mathrm {Hom}}_G(\Gamma _{\mathfrak {s}}, \pi )$
and
${\mathrm {Hom}}_G(\Gamma _{\mathfrak {s}}, \pi )$
and
![]() ${\mathrm {Hom}}_G(\Gamma _{\mathfrak {s}}, \pi ^-)$
.
${\mathrm {Hom}}_G(\Gamma _{\mathfrak {s}}, \pi ^-)$
.
For any unramified character
![]() $\chi $
, we have the specialization map
$\chi $
, we have the specialization map
![]() ${\text {sp}_{\chi } : \Gamma _{\mathfrak {s}} \mapsto i_P^G(\chi \rho \otimes \tau )}$
(cf. [Reference Heiermann17, Section 3.1]). The unique (up to scalar multiple) element of
${\text {sp}_{\chi } : \Gamma _{\mathfrak {s}} \mapsto i_P^G(\chi \rho \otimes \tau )}$
(cf. [Reference Heiermann17, Section 3.1]). The unique (up to scalar multiple) element of
![]() ${\mathrm {Hom}}_G(\Gamma _{\mathfrak {s}}, \pi )$
factors through
${\mathrm {Hom}}_G(\Gamma _{\mathfrak {s}}, \pi )$
factors through
![]() $\text {sp}_1 : \Gamma _{\mathfrak {s}} \to i_P^G(\rho \otimes \tau )$
; similarly, any element of
$\text {sp}_1 : \Gamma _{\mathfrak {s}} \to i_P^G(\rho \otimes \tau )$
; similarly, any element of
![]() ${\mathrm {Hom}}_G(\Gamma _{\mathfrak {s}}, \pi ^-)$
factors through
${\mathrm {Hom}}_G(\Gamma _{\mathfrak {s}}, \pi ^-)$
factors through
![]() $\text {sp}_{\chi _0}$
(recall that
$\text {sp}_{\chi _0}$
(recall that
![]() $\rho ^- = \chi _0\otimes \rho $
). Notice that
$\rho ^- = \chi _0\otimes \rho $
). Notice that
![]() $\Lambda _1$
and
$\Lambda _1$
and
![]() $\Lambda _{\chi _0}$
are the Whittaker models of
$\Lambda _{\chi _0}$
are the Whittaker models of
![]() $\pi $
and
$\pi $
and
![]() $\pi ^-$
, respectively.
$\pi ^-$
, respectively.
To determine the action of T on
![]() $\Lambda _{\chi }$
(for any
$\Lambda _{\chi }$
(for any
![]() $\chi $
), we must compare
$\chi $
), we must compare
![]() $\Lambda _{\chi }\text {sp}_{\chi }$
and
$\Lambda _{\chi }\text {sp}_{\chi }$
and
![]() $\Lambda _{\chi } \circ \text {sp}_{\chi } \circ T$
. The operator T is defined by the following property:
$\Lambda _{\chi } \circ \text {sp}_{\chi } \circ T$
. The operator T is defined by the following property:
(cf. [Reference Heiermann17, Sections 3.1 and 3.2]). Here,
![]() $J(\chi ^{-1})$
denotes the standard intertwining operator
$J(\chi ^{-1})$
denotes the standard intertwining operator
![]() $i_P^G(\chi ^{-1}\rho \otimes \tau ) \to i_P^G(\chi \rho ^{\vee } \otimes \tau )$
. To explain
$i_P^G(\chi ^{-1}\rho \otimes \tau ) \to i_P^G(\chi \rho ^{\vee } \otimes \tau )$
. To explain
![]() $\varphi $
, recall that
$\varphi $
, recall that
![]() $\rho $
is assumed to be self-dual. Therefore, we can fix an isomorphism
$\rho $
is assumed to be self-dual. Therefore, we can fix an isomorphism
![]() $\varphi : \rho ^{\vee } \mapsto \rho $
and induce to an isomorphism
$\varphi : \rho ^{\vee } \mapsto \rho $
and induce to an isomorphism
![]() $i_P^G(\chi \rho ^{\vee } \otimes \tau ) \to i_P^G(\chi \rho \otimes \tau )$
for any unramified
$i_P^G(\chi \rho ^{\vee } \otimes \tau ) \to i_P^G(\chi \rho \otimes \tau )$
for any unramified
![]() $\chi $
, which we again denote by
$\chi $
, which we again denote by
![]() $\varphi $
by abuse of notation.
$\varphi $
by abuse of notation.
Let
![]() $\Lambda _{\chi }^{\vee }$
denote the Whittaker functional on
$\Lambda _{\chi }^{\vee }$
denote the Whittaker functional on
![]() $i_P^G(\chi \rho ^{\vee } \otimes \tau )$
obtained using (3.11) from a fixed Whittaker functional
$i_P^G(\chi \rho ^{\vee } \otimes \tau )$
obtained using (3.11) from a fixed Whittaker functional
![]() $\lambda ^{\vee }$
for
$\lambda ^{\vee }$
for
![]() $\rho ^{\vee }$
. By the uniqueness of Whittaker functionals,
$\rho ^{\vee }$
. By the uniqueness of Whittaker functionals,
![]() $\Lambda _{\chi } \circ \varphi = c\cdot \Lambda _{\chi }^{\vee }$
for some constant c. Furthermore, since
$\Lambda _{\chi } \circ \varphi = c\cdot \Lambda _{\chi }^{\vee }$
for some constant c. Furthermore, since
![]() $\varphi $
is induced from an isomorphism
$\varphi $
is induced from an isomorphism
![]() $\varphi : \rho ^{\vee } \mapsto \rho $
, it follows immediately that c does not depend on
$\varphi : \rho ^{\vee } \mapsto \rho $
, it follows immediately that c does not depend on
![]() $\chi $
. Therefore, we have
$\chi $
. Therefore, we have
Note that there is a natural way to normalize
![]() $\varphi $
in such a way that
$\varphi $
in such a way that
![]() $c = 1$
. We denote by
$c = 1$
. We denote by
![]() $g^{\tau }$
the transpose of an element
$g^{\tau }$
the transpose of an element
![]() $g \in GL_k(F)$
with respect to the antidiagonal (and with
$g \in GL_k(F)$
with respect to the antidiagonal (and with
![]() $g^{-\tau }$
its inverse). One can then define a new representation
$g^{-\tau }$
its inverse). One can then define a new representation
![]() $\rho _1$
by
$\rho _1$
by
![]() $\rho _1(g) = \rho (g^{-\tau })$
. This representation is isomorphic to the contragredient of
$\rho _1(g) = \rho (g^{-\tau })$
. This representation is isomorphic to the contragredient of
![]() $\rho $
; the advantage is that it acts on
$\rho $
; the advantage is that it acts on
![]() $V_{\rho }$
, the space of
$V_{\rho }$
, the space of
![]() $\rho $
. Furthermore, for any diagonal matrix (i.e., an element of the maximal torus)
$\rho $
. Furthermore, for any diagonal matrix (i.e., an element of the maximal torus)
![]() $t \in GL_k(F)$
, we may conjugate
$t \in GL_k(F)$
, we may conjugate
![]() $\rho _1$
to get
$\rho _1$
to get
![]() $\rho _2(g) = {}^t\rho _1(g) = \rho _1(t^{-1}gt)$
. Then
$\rho _2(g) = {}^t\rho _1(g) = \rho _1(t^{-1}gt)$
. Then
![]() $\rho _2 \cong \rho _1$
, and with a suitable choice of t,
$\rho _2 \cong \rho _1$
, and with a suitable choice of t,
![]() $\rho _2$
becomes
$\rho _2$
becomes
![]() $\psi $
-generic with the same Whittaker functional
$\psi $
-generic with the same Whittaker functional
![]() $\lambda $
. For example, assume that
$\lambda $
. For example, assume that
![]() $\psi $
is given by
$\psi $
is given by
where
![]() $\psi _0$
is a nontrivial additive character of F, and u is an upper-triangular unipotent matrix with entries
$\psi _0$
is a nontrivial additive character of F, and u is an upper-triangular unipotent matrix with entries
![]() $u_{1,2},\dotsc ,u_{k-1,k}$
above the main diagonal. Then one checks immediately that
$u_{1,2},\dotsc ,u_{k-1,k}$
above the main diagonal. Then one checks immediately that
![]() $t=\text {diag}(1,-1,\dotsc ,(-1)^{k-1})$
gives
$t=\text {diag}(1,-1,\dotsc ,(-1)^{k-1})$
gives
for any
![]() $v \in V_{\rho }$
. In short, we may assume that
$v \in V_{\rho }$
. In short, we may assume that
![]() $ \Lambda _{\chi } \circ \text {sp}_{\chi } \circ T = \Lambda _{\chi }^{\vee } \circ J(\chi ^{-1}) \circ \text {sp}_{\chi ^{-1}}$
.
$ \Lambda _{\chi } \circ \text {sp}_{\chi } \circ T = \Lambda _{\chi }^{\vee } \circ J(\chi ^{-1}) \circ \text {sp}_{\chi ^{-1}}$
.
This leads to the second choice we have to make in the construction of T: that of the normalization of the intertwining operator J. Here, we choose the standard normalization introduced by Shahidi (cf. [Reference Shahidi24, Theorem 3.1]). Under this assumption, we have
for every unramified character
![]() $\chi $
. Thus,
$\chi $
. Thus,
With this, we are ready to compare the action of T on
![]() $\pi $
and
$\pi $
and
![]() $\pi ^-$
. For
$\pi ^-$
. For
![]() $\pi $
, we specialize at
$\pi $
, we specialize at
![]() $\chi = 1$
; this gives us
$\chi = 1$
; this gives us
i.e., T acts trivially.
For
![]() $\pi ^-$
, we specialize at
$\pi ^-$
, we specialize at
![]() $\chi _0$
. We notice that
$\chi _0$
. We notice that
![]() $\chi _0^{-1} = \chi _0\eta $
for some character
$\chi _0^{-1} = \chi _0\eta $
for some character
![]() $\eta $
such that
$\eta $
such that
![]() $\eta \circ \rho \cong \rho $
. This shows that
$\eta \circ \rho \cong \rho $
. This shows that
![]() $\text {sp}_{\chi ^{-1}} = \phi _{\eta }\circ \text {sp}_{\chi _0}$
, where
$\text {sp}_{\chi ^{-1}} = \phi _{\eta }\circ \text {sp}_{\chi _0}$
, where
![]() $\phi _{\eta }$
is the isomorphism
$\phi _{\eta }$
is the isomorphism
![]() $\rho \mapsto \eta \otimes \rho $
defined in [Reference Heiermann17, Section 1.17] (again, we induce to
$\rho \mapsto \eta \otimes \rho $
defined in [Reference Heiermann17, Section 1.17] (again, we induce to
![]() $\phi _{\eta } : i_P^G(\rho \otimes \tau ) \to i_P^G(\eta \rho \otimes \tau )$
and abuse the notation). Finally, using the uniqueness of Whittaker functionals again, we see that
$\phi _{\eta } : i_P^G(\rho \otimes \tau ) \to i_P^G(\eta \rho \otimes \tau )$
and abuse the notation). Finally, using the uniqueness of Whittaker functionals again, we see that
![]() $\Lambda _{\chi \eta } \circ \phi _{\eta } = d\cdot \Lambda _{\chi }$
for some constant d which does not depend on
$\Lambda _{\chi \eta } \circ \phi _{\eta } = d\cdot \Lambda _{\chi }$
for some constant d which does not depend on
![]() $\chi $
. We can normalize
$\chi $
. We can normalize
![]() $\phi _{\eta }$
so that
$\phi _{\eta }$
so that
![]() $d=1$
; then we have
$d=1$
; then we have
Therefore, T acts trivially on
![]() $\pi ^-$
as well.
$\pi ^-$
as well.
To summarize, if we use Shahidi’s normalization of the standard intertwining operator, and normalize
![]() $\varphi $
as we did above, it follows that T acts trivially on both
$\varphi $
as we did above, it follows that T acts trivially on both
![]() $\pi $
and
$\pi $
and
![]() $\pi ^-$
. This implies that the Gelfand–Graev module is isomorphic to
$\pi ^-$
. This implies that the Gelfand–Graev module is isomorphic to
(see (3.10)), where
![]() $\epsilon _0(T_n) = 1$
. Note that this is analogous to our results in Case (iii), because
$\epsilon _0(T_n) = 1$
. Note that this is analogous to our results in Case (iii), because
![]() $T_n$
again acts by
$T_n$
again acts by
![]() $q^r$
, only this time
$q^r$
, only this time
![]() $r= 0$
.
$r= 0$
.
This completes our analysis of the structure of
![]() $\mathcal {H}$
. We conclude the section by providing an alternative proof for the following result of [Reference Bushnell and Henniart6].
$\mathcal {H}$
. We conclude the section by providing an alternative proof for the following result of [Reference Bushnell and Henniart6].
Corollary 3.8 We have
the center of
![]() $\mathcal {H}$
.
$\mathcal {H}$
.
Proof Obviously,
![]() $Z(\mathcal {H})$
is contained in
$Z(\mathcal {H})$
is contained in
![]() ${\mathrm {End}}_{\mathcal {H}}(\Pi )$
, so we need to prove that any element of
${\mathrm {End}}_{\mathcal {H}}(\Pi )$
, so we need to prove that any element of
![]() ${\mathrm {End}}_{\mathcal {H}}(\Pi )$
is given by a multiplication with an element
${\mathrm {End}}_{\mathcal {H}}(\Pi )$
is given by a multiplication with an element
![]() $f \in Z(\mathcal {H})$
. We prove the corollary in Case (iii); the proof in Cases (i) and (ii) is analogous.
$f \in Z(\mathcal {H})$
. We prove the corollary in Case (iii); the proof in Cases (i) and (ii) is analogous.
We start by recalling that
![]() $Z(\mathcal {H}) = \mathcal {A}^W$
, the Weyl group invariants of
$Z(\mathcal {H}) = \mathcal {A}^W$
, the Weyl group invariants of
![]() $\mathcal {A}$
. Note that any element of
$\mathcal {A}$
. Note that any element of
![]() ${\mathrm {End}}_{\mathcal {H}}(\Pi )$
can be viewed as an element of
${\mathrm {End}}_{\mathcal {H}}(\Pi )$
can be viewed as an element of
![]() $\mathcal {A}$
. Indeed, let
$\mathcal {A}$
. Indeed, let
![]() $f \in {\mathrm {End}}_{\mathcal {H}}(\Pi )$
. We have
$f \in {\mathrm {End}}_{\mathcal {H}}(\Pi )$
. We have
![]() ${\mathrm {End}}_{\mathcal {H}}(\Pi ) \subseteq {\mathrm {End}}_{\mathcal {A}}(\Pi )$
, but we know that
${\mathrm {End}}_{\mathcal {H}}(\Pi ) \subseteq {\mathrm {End}}_{\mathcal {A}}(\Pi )$
, but we know that
![]() $\Pi = \mathcal {A}$
as an
$\Pi = \mathcal {A}$
as an
![]() $\mathcal {A}$
-module. Therefore,
$\mathcal {A}$
-module. Therefore,
![]() $f \in {\mathrm {End}}_{\mathcal {A}}(\mathcal {A}) = \mathcal {A}$
. Thus, it remains to prove that f is invariant under the action of the Weyl group.
$f \in {\mathrm {End}}_{\mathcal {A}}(\mathcal {A}) = \mathcal {A}$
. Thus, it remains to prove that f is invariant under the action of the Weyl group.
It suffices to prove that f is invariant under the set of simple reflections which generate the Weyl group. In other words, we need to prove that
using the notation of Section 2.6. This follows immediately from what we now know about the structure of
![]() $\Pi $
as an
$\Pi $
as an
![]() $\mathcal {H}$
-module:
$\mathcal {H}$
-module:
![]() $\Pi = \mathcal {H} \otimes _{\mathcal {H}_0} \epsilon $
. In other words, we have shown that there exists an element
$\Pi = \mathcal {H} \otimes _{\mathcal {H}_0} \epsilon $
. In other words, we have shown that there exists an element
![]() $g\in \mathcal {A} \cong \Pi $
(constructed in Section 3.1) on which the elements
$g\in \mathcal {A} \cong \Pi $
(constructed in Section 3.1) on which the elements
![]() $T_1,\dotsc , T_{n-1}$
and
$T_1,\dotsc , T_{n-1}$
and
![]() $T_n$
act by scalar multiplication with
$T_n$
act by scalar multiplication with
![]() $q^t$
, and
$q^t$
, and
![]() $q^r$
, respectively.
$q^r$
, respectively.
We now look at the commutation relation
 $$\begin{align*}T_nf - f^{\vee} T_n = \left((q^r-1) + \frac{1}{X_n}(\sqrt{q}^{r+s}-\sqrt{q}^{r-s})\right)\frac{f - f^{\vee}}{1-1/X_n^2} \end{align*}$$
$$\begin{align*}T_nf - f^{\vee} T_n = \left((q^r-1) + \frac{1}{X_n}(\sqrt{q}^{r+s}-\sqrt{q}^{r-s})\right)\frac{f - f^{\vee}}{1-1/X_n^2} \end{align*}$$
satisfied by
![]() $T_n$
and f. Applying this to g (recall that
$T_n$
and f. Applying this to g (recall that
![]() $T_ng = q^rg$
), and using the fact that f is in
$T_ng = q^rg$
), and using the fact that f is in
![]() ${\mathrm {Hom}}_{\mathcal {H}}(\Pi )$
(so that
${\mathrm {Hom}}_{\mathcal {H}}(\Pi )$
(so that
![]() $T_nfg = fT_ng$
), we get
$T_nfg = fT_ng$
), we get
 $$\begin{align*}(f-f^{\vee})q^r\cdot g = \left((q^r-1) + \frac{1}{X_n}(\sqrt{q}^{r+s}-\sqrt{q}^{r-s})\right)\frac{f - f^{\vee}}{1-1/X_n^2}\cdot g. \end{align*}$$
$$\begin{align*}(f-f^{\vee})q^r\cdot g = \left((q^r-1) + \frac{1}{X_n}(\sqrt{q}^{r+s}-\sqrt{q}^{r-s})\right)\frac{f - f^{\vee}}{1-1/X_n^2}\cdot g. \end{align*}$$
This is an equality in
![]() $\mathcal {A}$
. Since
$\mathcal {A}$
. Since
![]() $q^r \neq \left ((q^r-1) + \frac {1}{X_n}(\sqrt {q}^{r+s}-\sqrt {q}^{r-s})\right )\frac {1}{1-1/X_n^2}$
and
$q^r \neq \left ((q^r-1) + \frac {1}{X_n}(\sqrt {q}^{r+s}-\sqrt {q}^{r-s})\right )\frac {1}{1-1/X_n^2}$
and
![]() ${g\neq 0}$
, it follows that
${g\neq 0}$
, it follows that
![]() $f-f^{\vee }$
must be
$f-f^{\vee }$
must be
![]() $0$
. Therefore,
$0$
. Therefore,
![]() $f = f^{\vee }$
. We get
$f = f^{\vee }$
. We get
![]() $f = f^{s_i}$
in the same way, using the commutation relations satisfied by the operators
$f = f^{s_i}$
in the same way, using the commutation relations satisfied by the operators
![]() $T_i$
. This proves the corollary.
$T_i$
. This proves the corollary.
4 An application to the GGP restriction problem
The theory of Bernstein–Zelevinsky derivatives implies that the restriction of an irreducible supercuspidal representation
![]() $\sigma $
of
$\sigma $
of
![]() $\mathrm {GL}(n+1)$
to
$\mathrm {GL}(n+1)$
to
![]() $\mathrm {GL}(n)$
is isomorphic to the Gelfand–Graev representation of
$\mathrm {GL}(n)$
is isomorphic to the Gelfand–Graev representation of
![]() $\mathrm {GL}(n)$
. Thus, given a maximal ideal
$\mathrm {GL}(n)$
. Thus, given a maximal ideal
![]() $\mathcal J$
in the Bernstein center of
$\mathcal J$
in the Bernstein center of
![]() $\mathrm {GL}(n)$
, there exists only one irreducible
$\mathrm {GL}(n)$
, there exists only one irreducible
![]() $\mathrm {GL}(n)$
-quotient of
$\mathrm {GL}(n)$
-quotient of
![]() $\sigma $
annihilated by
$\sigma $
annihilated by
![]() $\mathcal J$
. The goal of this short section is to show that a similar statement holds when restricting a cuspidal representation of an orthogonal group
$\mathcal J$
. The goal of this short section is to show that a similar statement holds when restricting a cuspidal representation of an orthogonal group
![]() $\mathrm {O}(m+1)$
to a subgroup
$\mathrm {O}(m+1)$
to a subgroup
![]() $\mathrm {O}(m) \subset \mathrm {O}(m+1)$
.
$\mathrm {O}(m) \subset \mathrm {O}(m+1)$
.
Lemma 4.1 Let
![]() $\sigma $
be an irreducible representation of
$\sigma $
be an irreducible representation of
![]() $\mathrm {O}(m+1)$
. For any inertial data
$\mathrm {O}(m+1)$
. For any inertial data
![]() $\mathfrak s$
of
$\mathfrak s$
of
![]() $\mathrm {O}(m)$
, let
$\mathrm {O}(m)$
, let
![]() $\sigma [\mathfrak s]$
be the corresponding Bernstein summand of
$\sigma [\mathfrak s]$
be the corresponding Bernstein summand of
![]() $\sigma $
. We have:
$\sigma $
. We have:
-
• If
 $\sigma $
is supercuspidal, then it is a projective
$\sigma $
is supercuspidal, then it is a projective
 $\mathrm {O}(m)$
-module.
$\mathrm {O}(m)$
-module. -
•
 $\mathrm {dim} \,{\mathrm {Hom}}_{\mathrm {O}(m)}(\sigma , \pi ) \leq 1$
for any irreducible representation
$\mathrm {dim} \,{\mathrm {Hom}}_{\mathrm {O}(m)}(\sigma , \pi ) \leq 1$
for any irreducible representation
 $\pi $
of
$\pi $
of
 $\mathrm {O}(m)$
.
$\mathrm {O}(m)$
. -
•
 $\sigma [\mathfrak s]$
is a finitely generated
$\sigma [\mathfrak s]$
is a finitely generated
 $\mathrm {O}(m)$
-module.
$\mathrm {O}(m)$
-module.
The same conclusions hold if we replace orthogonal by special orthogonal groups.
Proof The first statement is an observation:
![]() $\sigma $
is a direct summand of
$\sigma $
is a direct summand of
![]() ${C_c^{\infty }(\mathrm {O}(m+1))}$
(the space of locally constant and compactly supported functions on
${C_c^{\infty }(\mathrm {O}(m+1))}$
(the space of locally constant and compactly supported functions on
![]() $\mathrm {O}(m+1)$
) and
$\mathrm {O}(m+1)$
) and
![]() $C_c^{\infty }(\mathrm {O}(m+1))$
stays projective after restriction to
$C_c^{\infty }(\mathrm {O}(m+1))$
stays projective after restriction to
![]() $\mathrm {O}(m)$
. The second is the multiplicity one theorem [Reference Aizenbud, Gourevitch, Rallis and Schiffmann2]. For the third, observe that we have a surjection
$\mathrm {O}(m)$
. The second is the multiplicity one theorem [Reference Aizenbud, Gourevitch, Rallis and Schiffmann2]. For the third, observe that we have a surjection
By Theorem A of [Reference Aizenbud, Avni and Gourevitch1] or Remark 5.1.7 of [Reference Sakellaridis and Venkatesh23], the Bernstein components of
![]() $C_c^{\infty }(\mathrm {O}(m+1))$
, considered as an
$C_c^{\infty }(\mathrm {O}(m+1))$
, considered as an
![]() $\mathrm {O}(m+1) \times \mathrm {O}(m)$
-module, are finitely generated. The third bullet now follows at once.
$\mathrm {O}(m+1) \times \mathrm {O}(m)$
-module, are finitely generated. The third bullet now follows at once.
The following is the main result of this section.
Proposition 4.2 Let
![]() $\sigma $
be an irreducible supercuspidal representation of
$\sigma $
be an irreducible supercuspidal representation of
![]() $\mathrm {O}(m+1)$
. Let
$\mathrm {O}(m+1)$
. Let
![]() $\mathfrak s$
be inertial data for a subgroup
$\mathfrak s$
be inertial data for a subgroup
![]() $\mathrm {O}(m) \subset \mathrm {O}(m+1)$
such that
$\mathrm {O}(m) \subset \mathrm {O}(m+1)$
such that
![]() $\sigma [\mathfrak s]\neq 0$
. Let
$\sigma [\mathfrak s]\neq 0$
. Let
![]() $\mathcal Z$
be the center of the Bernstein component corresponding
$\mathcal Z$
be the center of the Bernstein component corresponding
![]() $\mathfrak s$
. The block
$\mathfrak s$
. The block
![]() $\sigma [\mathfrak s]$
is indecomposable, and for every maximal ideal
$\sigma [\mathfrak s]$
is indecomposable, and for every maximal ideal
![]() $\mathcal J$
in
$\mathcal J$
in
![]() $\mathcal Z$
, there exists unique irreducible representation
$\mathcal Z$
, there exists unique irreducible representation
![]() $\pi $
of
$\pi $
of
![]() $\mathrm {O}(m)$
annihilated by
$\mathrm {O}(m)$
annihilated by
![]() $\mathcal J$
such that
$\mathcal J$
such that
![]() ${\mathrm {Hom}}_{\mathrm {O}(m)}(\sigma , \pi ) \cong {\mathbb C}$
.
${\mathrm {Hom}}_{\mathrm {O}(m)}(\sigma , \pi ) \cong {\mathbb C}$
.
Proof Assume that m is even. Let
![]() $\Gamma _{\mathfrak s}$
be the projective generator associated with the inertial data
$\Gamma _{\mathfrak s}$
be the projective generator associated with the inertial data
![]() $\mathfrak s$
, and let
$\mathfrak s$
, and let
![]() ${\mathcal H}$
be the algebra of endomorphisms of
${\mathcal H}$
be the algebra of endomorphisms of
![]() $\Gamma _{\mathfrak s}$
. Since
$\Gamma _{\mathfrak s}$
. Since
![]() $\sigma [\mathfrak s]\neq 0$
, combining the above lemma and Remark 3.2, one concludes that
$\sigma [\mathfrak s]\neq 0$
, combining the above lemma and Remark 3.2, one concludes that
as
![]() $\mathcal A$
-modules, proving indecomposability of the block, and then by Corollary 3.7
$\mathcal A$
-modules, proving indecomposability of the block, and then by Corollary 3.7
for some finite subalgebra
![]() ${\mathcal H}_W \cong {\mathbb C}[W]$
, where W is a finite group, such that
${\mathcal H}_W \cong {\mathbb C}[W]$
, where W is a finite group, such that
![]() ${\mathcal H} \cong \mathcal A \otimes {\mathcal H}_W$
and
${\mathcal H} \cong \mathcal A \otimes {\mathcal H}_W$
and
![]() $\mathcal A^W$
is the center
$\mathcal A^W$
is the center
![]() $\mathcal Z$
of
$\mathcal Z$
of
![]() ${\mathcal H}$
, that is, the center of the Bernstein component corresponding to
${\mathcal H}$
, that is, the center of the Bernstein component corresponding to
![]() $\mathfrak s$
.
$\mathfrak s$
.
Now, recall that all irreducible representations annihilated by
![]() $\mathcal J$
are subquotients of a single principal series representation
$\mathcal J$
are subquotients of a single principal series representation
where
![]() $\chi $
is a character of
$\chi $
is a character of
![]() $\mathcal A$
. Observe that the principal series is isomorphic to
$\mathcal A$
. Observe that the principal series is isomorphic to
![]() ${\mathcal H}_W\cong {\mathbb C}[W]$
as an
${\mathcal H}_W\cong {\mathbb C}[W]$
as an
![]() ${\mathcal H}_W$
-module. Since the one-dimensional type
${\mathcal H}_W$
-module. Since the one-dimensional type
![]() $\epsilon $
appears with multiplicity one in
$\epsilon $
appears with multiplicity one in
![]() ${\mathcal H}_W$
, there exists unique irreducible representation annihilated by
${\mathcal H}_W$
, there exists unique irreducible representation annihilated by
![]() $\mathcal J$
containing the type
$\mathcal J$
containing the type
![]() $\epsilon $
. But precisely, these representations are irreducible quotients of
$\epsilon $
. But precisely, these representations are irreducible quotients of
![]() ${\mathcal H} \otimes _{{\mathcal H}_W} \epsilon $
, by the Frobenius reciprocity.
${\mathcal H} \otimes _{{\mathcal H}_W} \epsilon $
, by the Frobenius reciprocity.
Now, assume that m is odd. In this case, we shall derive the result working with
![]() $\mathrm {SO}(m)$
and its Hecke algebras. Observe that
$\mathrm {SO}(m)$
and its Hecke algebras. Observe that
![]() $\mathrm {O}(m)= \mathrm {SO}(m) \times \{\pm 1_m\}$
, so representations of
$\mathrm {O}(m)= \mathrm {SO}(m) \times \{\pm 1_m\}$
, so representations of
![]() $\mathrm {O}(m)$
and
$\mathrm {O}(m)$
and
![]() $\mathrm {SO}(m)$
are easy to relate. Let
$\mathrm {SO}(m)$
are easy to relate. Let
![]() $\mathfrak s_0$
be the restriction to
$\mathfrak s_0$
be the restriction to
![]() $\mathrm {SO}(m)$
of the inertial data
$\mathrm {SO}(m)$
of the inertial data
![]() $\mathfrak s$
. On the other hand, the inertial data
$\mathfrak s$
. On the other hand, the inertial data
![]() $\mathfrak s_0$
give a pair of inertial data
$\mathfrak s_0$
give a pair of inertial data
![]() $\mathfrak s^{\pm }$
of
$\mathfrak s^{\pm }$
of
![]() $\mathrm {O}(m)$
by specifying how
$\mathrm {O}(m)$
by specifying how
![]() $-1_m$
acts. Let
$-1_m$
acts. Let
![]() $\sigma _0$
be the restriction of
$\sigma _0$
be the restriction of
![]() $\sigma $
to
$\sigma $
to
![]() $\mathrm {SO}(m+1)$
. We have two cases. Assume that
$\mathrm {SO}(m+1)$
. We have two cases. Assume that
![]() $\sigma _0$
is irreducible. Then we can apply the above lemma to special orthogonal groups to prove the proposition for special orthogonal groups, that is,
$\sigma _0$
is irreducible. Then we can apply the above lemma to special orthogonal groups to prove the proposition for special orthogonal groups, that is,
![]() $\sigma _0[\mathfrak s_0]$
is indecomposable and has an explicit
$\sigma _0[\mathfrak s_0]$
is indecomposable and has an explicit
![]() ${\mathcal H}$
-structure by Corollary 3.7. Now, observe that
${\mathcal H}$
-structure by Corollary 3.7. Now, observe that
![]() $-1_m\in \mathrm {O}(m)$
naturally acts on
$-1_m\in \mathrm {O}(m)$
naturally acts on
![]() $\sigma _0[\mathfrak s_0]$
. By indecomposability of
$\sigma _0[\mathfrak s_0]$
. By indecomposability of
![]() $\sigma _0[\mathfrak s_0]$
,
$\sigma _0[\mathfrak s_0]$
,
![]() $-1_m$
has to act by the same scalar on whole block. Therefore, either
$-1_m$
has to act by the same scalar on whole block. Therefore, either
![]() $\sigma [\mathfrak s^+]\neq 0$
or
$\sigma [\mathfrak s^+]\neq 0$
or
![]() $\sigma [\mathfrak s^-]\neq 0$
and proposition holds in this case, for whichever of this two blocks is nontrivial. Now, assume that
$\sigma [\mathfrak s^-]\neq 0$
and proposition holds in this case, for whichever of this two blocks is nontrivial. Now, assume that
![]() $\sigma _0$
is reducible. Then
$\sigma _0$
is reducible. Then
![]() $\sigma \otimes \det \cong \sigma $
. Decompose
$\sigma \otimes \det \cong \sigma $
. Decompose
![]() $\sigma = \sigma ^+ \oplus \sigma ^-$
where
$\sigma = \sigma ^+ \oplus \sigma ^-$
where
![]() $-1_m$
acts by
$-1_m$
acts by
![]() $1$
and
$1$
and
![]() $-1$
on the two summands. Since
$-1$
on the two summands. Since
![]() $\sigma \otimes \det \cong \sigma $
, it follows that
$\sigma \otimes \det \cong \sigma $
, it follows that
![]() $\sigma ^+$
and
$\sigma ^+$
and
![]() $\sigma ^-$
are isomorphic multiplicity-free, projective
$\sigma ^-$
are isomorphic multiplicity-free, projective
![]() $\mathrm {SO}(m)$
-modules. Now, arguing as before, it follows that the proposition holds for both components
$\mathrm {SO}(m)$
-modules. Now, arguing as before, it follows that the proposition holds for both components
![]() $\sigma [\mathfrak s^+]\neq 0$
and
$\sigma [\mathfrak s^+]\neq 0$
and
![]() $\sigma [\mathfrak s^-]\neq 0$
.
$\sigma [\mathfrak s^-]\neq 0$
.
Note that the above result is compatible with Gan–Gross–Prasad conjectures [Reference Gan, Gross and Prasad13], and it sheds some light on the restriction problem beyond tempered representations. Of course, the above proposition holds for any
![]() $\sigma $
that is projective as an
$\sigma $
that is projective as an
![]() $\mathrm {O}(m)$
-module. It would be interesting to classify irreducible
$\mathrm {O}(m)$
-module. It would be interesting to classify irreducible
![]() $\sigma $
that are projective when restricted to
$\sigma $
that are projective when restricted to
![]() $\mathrm {O}(m)$
. Projectivity of restriction from
$\mathrm {O}(m)$
. Projectivity of restriction from
![]() $\mathrm {GL}(n+1)$
to
$\mathrm {GL}(n+1)$
to
![]() $\mathrm {GL}(n)$
was studied in [Reference Chan and Savin12], and a complete classification of irreducible representations of
$\mathrm {GL}(n)$
was studied in [Reference Chan and Savin12], and a complete classification of irreducible representations of
![]() $\mathrm {GL}(n+1)$
that are projective as
$\mathrm {GL}(n+1)$
that are projective as
![]() $\mathrm {GL}(n)$
-modules was obtained in [Reference Chan9].
$\mathrm {GL}(n)$
-modules was obtained in [Reference Chan9].
Appendix A An isomorphism of projective generators
Let G be a reductive group, and let
![]() $\mathfrak {s}$
be an inertial class of cuspidal data
$\mathfrak {s}$
be an inertial class of cuspidal data
![]() $(M,\sigma )$
, where M is a Levi subgroup of G. Now, recall the Bushnell–Kutzko theory of types [Reference Bushnell and Kutzko8]: Any such
$(M,\sigma )$
, where M is a Levi subgroup of G. Now, recall the Bushnell–Kutzko theory of types [Reference Bushnell and Kutzko8]: Any such
![]() $\mathfrak {s}$
is expected to have a type
$\mathfrak {s}$
is expected to have a type
![]() $(J,\lambda )$
, where J is a compact subgroup of G, and
$(J,\lambda )$
, where J is a compact subgroup of G, and
![]() $\lambda $
is an irreducible representation of J such that
$\lambda $
is an irreducible representation of J such that
![]() ${\mathrm {c-ind}}_J^G \lambda $
is a projective generator for
${\mathrm {c-ind}}_J^G \lambda $
is a projective generator for
![]() $\text {Rep}_{\mathfrak {s}}(G)$
. One is interested in the structure of the Hecke algebra
$\text {Rep}_{\mathfrak {s}}(G)$
. One is interested in the structure of the Hecke algebra
![]() $\mathcal {H}(G,\lambda )= {\mathrm {End}}_G({\mathrm {c-ind}}_J^G \lambda )$
. In this section, we show that, under certain conditions (when
$\mathcal {H}(G,\lambda )= {\mathrm {End}}_G({\mathrm {c-ind}}_J^G \lambda )$
. In this section, we show that, under certain conditions (when
![]() $(J,\lambda )$
exists), the Hecke algebra
$(J,\lambda )$
exists), the Hecke algebra
![]() $\mathcal {H}(G,\lambda )={\mathrm {End}}_G({\mathrm {c-ind}}_J^G \lambda )$
is isomorphic to the algebra
$\mathcal {H}(G,\lambda )={\mathrm {End}}_G({\mathrm {c-ind}}_J^G \lambda )$
is isomorphic to the algebra
![]() $\mathcal {H}_{\mathfrak {s}} = {\mathrm {End}}_G(\Gamma _{\mathfrak {s}})$
constructed in Section 2.4. More precisely, we have the following:
$\mathcal {H}_{\mathfrak {s}} = {\mathrm {End}}_G(\Gamma _{\mathfrak {s}})$
constructed in Section 2.4. More precisely, we have the following:
Theorem A.1 Assume that G is a classical group and that the residue characteristic of F is different from
![]() $2$
. Let
$2$
. Let
![]() $\mathfrak {s}=[(M,\sigma )]$
be an inertial equivalence class in G. There exists an
$\mathfrak {s}=[(M,\sigma )]$
be an inertial equivalence class in G. There exists an
![]() $\mathfrak {s}$
-type
$\mathfrak {s}$
-type
![]() $(J,\lambda )$
such that the generators
$(J,\lambda )$
such that the generators
![]() $\Gamma _{\mathfrak {s}}$
and
$\Gamma _{\mathfrak {s}}$
and
![]() ${\mathrm {c-ind}}_J^G\lambda $
are isomorphic.
${\mathrm {c-ind}}_J^G\lambda $
are isomorphic.
We break up the main part of the proof into three auxiliary results (see Lemmas A.2–A.4) which hold for arbitrary reductive p-adic groups. We use the theory of covers developed by Bushnell and Kutzko. Any inertial equivalence class
![]() $\mathfrak {s} = [(M,\sigma )]$
in G also determines a (cuspidal) inertial equivalence class
$\mathfrak {s} = [(M,\sigma )]$
in G also determines a (cuspidal) inertial equivalence class
![]() $\mathfrak {s}_M = [(M,\sigma )]$
in M. Let
$\mathfrak {s}_M = [(M,\sigma )]$
in M. Let
![]() $(J,\lambda )$
be a type for
$(J,\lambda )$
be a type for
![]() $\mathfrak {s}$
, and let
$\mathfrak {s}$
, and let
![]() $(J_M,\lambda _M)$
be a type for
$(J_M,\lambda _M)$
be a type for
![]() $\mathfrak {s}_M$
. We say that the
$\mathfrak {s}_M$
. We say that the
![]() $(J,\lambda )$
is a cover of the type
$(J,\lambda )$
is a cover of the type
![]() $(J_M,\lambda _M)$
if J decomposes with respect to M (in particular,
$(J_M,\lambda _M)$
if J decomposes with respect to M (in particular,
![]() $J_M = J \cap M$
and
$J_M = J \cap M$
and
![]() $\lambda _M = \lambda |_M$
) and the equivalence of categories
$\lambda _M = \lambda |_M$
) and the equivalence of categories
![]() $\text {Rep}_{\mathfrak {s}}(G) \to \mathcal {H}(G,\lambda )$
-Mod commutes with parabolic induction and the Jacquet functor in the appropriate sense (see Definition 8.1 and paragraph 5 of Introduction of [Reference Bushnell and Kutzko8]). We then have the following.
$\text {Rep}_{\mathfrak {s}}(G) \to \mathcal {H}(G,\lambda )$
-Mod commutes with parabolic induction and the Jacquet functor in the appropriate sense (see Definition 8.1 and paragraph 5 of Introduction of [Reference Bushnell and Kutzko8]). We then have the following.
Lemma A.2 (Theorem 7.9(iii) of [Reference Bushnell and Kutzko8])
Let P be any parabolic subgroup with Levi factor M. For any smooth representation
![]() $V \in \mathrm {Rep}(G)$
, the Jacquet functor with respect to P induces an isomorphism
$V \in \mathrm {Rep}(G)$
, the Jacquet functor with respect to P induces an isomorphism
Here,
![]() $V^{\lambda }$
denotes the
$V^{\lambda }$
denotes the
![]() $\lambda $
-isotype of V, i.e., the sum of all G-invariant subspaces of V isomorphic to
$\lambda $
-isotype of V, i.e., the sum of all G-invariant subspaces of V isomorphic to
![]() $\lambda $
.
$\lambda $
.
We use this to reduce the proof of Theorem A.1 to the case of cuspidal components.
Lemma A.3 Let
![]() $(J,\lambda )$
be a type for
$(J,\lambda )$
be a type for
![]() $\mathfrak {s} = [(M,\pi )]$
in G, and let
$\mathfrak {s} = [(M,\pi )]$
in G, and let
![]() $(J_M,\lambda _M)$
be a type for
$(J_M,\lambda _M)$
be a type for
![]() $\mathfrak {s}_M = [(M,\pi )]$
in M. Assume that
$\mathfrak {s}_M = [(M,\pi )]$
in M. Assume that
![]() $(J,\lambda )$
is a cover of
$(J,\lambda )$
is a cover of
![]() $(J_M,\lambda _M)$
.
$(J_M,\lambda _M)$
.
If the Bernstein generator
![]() $\Gamma _{\mathfrak {s}_M}$
is isomorphic to the Bushnell–Kutzko generator
$\Gamma _{\mathfrak {s}_M}$
is isomorphic to the Bushnell–Kutzko generator
![]() ${\mathrm {c-ind}}_{J_M}^M \lambda _M$
for the cuspidal component
${\mathrm {c-ind}}_{J_M}^M \lambda _M$
for the cuspidal component
![]() $\mathrm {Rep}_{\mathfrak {s}_M}(M)$
, then we also have an isomorphism of generators for the component
$\mathrm {Rep}_{\mathfrak {s}_M}(M)$
, then we also have an isomorphism of generators for the component
![]() $\mathrm {Rep}_{\mathfrak {s}}(G)$
.
$\mathrm {Rep}_{\mathfrak {s}}(G)$
.
Proof Lemma A.2 shows that we have
for any G-module V. Here,
![]() ${\mathrm {Res}}_H^G$
denotes the restriction functor from G to H, and
${\mathrm {Res}}_H^G$
denotes the restriction functor from G to H, and
![]() $r_N$
denotes the Jacquet functor with respect to
$r_N$
denotes the Jacquet functor with respect to
![]() $P = MN$
. In other words, we get the following isomorphism of functors
$P = MN$
. In other words, we get the following isomorphism of functors
![]() $\text {Rep}(G) \to \text {Rep}(J_M)$
:
$\text {Rep}(G) \to \text {Rep}(J_M)$
:
where we have used
![]() $\lambda \text {-iso}$
(resp.
$\lambda \text {-iso}$
(resp.
![]() $\lambda _M\text {-iso}$
) to denote taking the
$\lambda _M\text {-iso}$
) to denote taking the
![]() $\lambda $
- (resp.
$\lambda $
- (resp.
![]() $\lambda _M$
-) isotype.
$\lambda _M$
-) isotype.
All of the above functors have left adjoints:
-
–
 ${\mathrm {c-ind}}_{J_M}^J$
and
${\mathrm {c-ind}}_{J_M}^J$
and
 ${\mathrm {c-ind}}_{J_M}^M$
for
${\mathrm {c-ind}}_{J_M}^M$
for
 ${\mathrm {Res}}_{J_M}^J$
and
${\mathrm {Res}}_{J_M}^J$
and
 ${\mathrm {Res}}_{J_M}^M$
, respectively;
${\mathrm {Res}}_{J_M}^M$
, respectively; -
–
 $i_{\overline {P}}^G$
for
$i_{\overline {P}}^G$
for
 $r_N$
(this is the Bernstein form of Frobenius reciprocity; here,
$r_N$
(this is the Bernstein form of Frobenius reciprocity; here,
 $\overline {P} = M\overline {N}$
is the parabolic subgroup opposite to P);
$\overline {P} = M\overline {N}$
is the parabolic subgroup opposite to P); -
–
 $\lambda $
-iso and
$\lambda $
-iso and
 $\lambda _M$
-iso are self-adjoint, because we are working with (necessarily semisimple) representations of compact groups J and
$\lambda _M$
-iso are self-adjoint, because we are working with (necessarily semisimple) representations of compact groups J and
 $J_M$
.
$J_M$
.
Since adjoints are unique (up to equivalence), taking the adjoint of (*), we get
We now apply both sides of the above equality to
![]() $\lambda _M$
. On the right-hand side, we get
$\lambda _M$
. On the right-hand side, we get
![]() $i_{\overline {P}}^G({\mathrm {c-ind}}_{J_M}^M \lambda _M)$
. By the assumptions from the statement of the lemma, we have
$i_{\overline {P}}^G({\mathrm {c-ind}}_{J_M}^M \lambda _M)$
. By the assumptions from the statement of the lemma, we have
![]() ${\mathrm {c-ind}}_{J_M}^M \lambda _M =\Gamma _{s_M}$
; therefore,
${\mathrm {c-ind}}_{J_M}^M \lambda _M =\Gamma _{s_M}$
; therefore,
![]() $i_{\overline {P}}^G({\mathrm {c-ind}}_{J_M}^M \lambda _M)$
is exactly the Bernstein generator
$i_{\overline {P}}^G({\mathrm {c-ind}}_{J_M}^M \lambda _M)$
is exactly the Bernstein generator
![]() $i_{\overline {P}}^G(\Gamma _{s_M}) = \Gamma _s$
. Here, we used the fact that the construction of the Bernstein generator does not depend on the choice of parabolic P (we choose
$i_{\overline {P}}^G(\Gamma _{s_M}) = \Gamma _s$
. Here, we used the fact that the construction of the Bernstein generator does not depend on the choice of parabolic P (we choose
![]() $\overline {P}$
) with fixed Levi M (cf. [Reference Bernstein4, Proposition 35]).
$\overline {P}$
) with fixed Levi M (cf. [Reference Bernstein4, Proposition 35]).
On the left-hand side, we get
![]() ${\mathrm {c-ind}}_{J}^G(({\mathrm {c-ind}}_{J_M}^J \lambda _M)^{\lambda })$
. However, Frobenius reciprocity gives us
${\mathrm {c-ind}}_{J}^G(({\mathrm {c-ind}}_{J_M}^J \lambda _M)^{\lambda })$
. However, Frobenius reciprocity gives us
![]() $\dim {\mathrm {Hom}}_J({\mathrm {c-ind}}_{J_M}^J \lambda _M, \lambda ) = \dim {\mathrm {Hom}}_{J_M}(\lambda _M, \lambda |_M) = 1$
, which follows from
$\dim {\mathrm {Hom}}_J({\mathrm {c-ind}}_{J_M}^J \lambda _M, \lambda ) = \dim {\mathrm {Hom}}_{J_M}(\lambda _M, \lambda |_M) = 1$
, which follows from
![]() $\lambda |_M = \lambda _M$
. Therefore,
$\lambda |_M = \lambda _M$
. Therefore,
![]() $({\mathrm {c-ind}}_{J_M}^J \lambda _M)^{\lambda } = \lambda $
, and the left-hand side becomes
$({\mathrm {c-ind}}_{J_M}^J \lambda _M)^{\lambda } = \lambda $
, and the left-hand side becomes
![]() ${\mathrm {c-ind}}_{J}^G(\lambda )$
, i.e., the Bushnell–Kutzko generator. Thus,
${\mathrm {c-ind}}_{J}^G(\lambda )$
, i.e., the Bushnell–Kutzko generator. Thus,
as claimed.
The above lemma allows us to focus on cuspidal components of the form
![]() $\mathfrak {s}_M = [(M,\sigma )]$
in M. If we want to prove the isomorphism of generators in general, it remains to prove that the generators of the cuspidal components are isomorphic. In other words, we would like to show that
$\mathfrak {s}_M = [(M,\sigma )]$
in M. If we want to prove the isomorphism of generators in general, it remains to prove that the generators of the cuspidal components are isomorphic. In other words, we would like to show that
where
![]() $\sigma _0$
is an (any) irreducible constituent of
$\sigma _0$
is an (any) irreducible constituent of
![]() $\sigma |_{M^{\circ }}$
. We shall accomplish this under the following assumptions. Assume that
$\sigma |_{M^{\circ }}$
. We shall accomplish this under the following assumptions. Assume that
where (see (5.5) in [Reference Bushnell and Kutzko8]):
-
•
 $\tilde J_M$
is compact modulo center subgroup of M such that
$\tilde J_M$
is compact modulo center subgroup of M such that
 $J_M = \tilde J_M \cap M^{\circ }$
,
$J_M = \tilde J_M \cap M^{\circ }$
, -
• the restriction of
 $\tilde \lambda _M$
to
$\tilde \lambda _M$
to
 $J_M$
is
$J_M$
is
 $\lambda _M$
,
$\lambda _M$
, -
• any
 $x\in M$
which intertwines the representation
$x\in M$
which intertwines the representation
 $\lambda _M$
belongs to
$\lambda _M$
belongs to
 $\tilde J_M$
.
$\tilde J_M$
.
Lemma A.4 Let
![]() $\sigma ={\mathrm {c-ind}}^M_{\tilde J_M} \tilde \lambda _M $
be a cuspidal representation of M where the pair
$\sigma ={\mathrm {c-ind}}^M_{\tilde J_M} \tilde \lambda _M $
be a cuspidal representation of M where the pair
![]() $(\tilde J_M, \tilde \lambda _M)$
satisfies the above three bullets. Then
$(\tilde J_M, \tilde \lambda _M)$
satisfies the above three bullets. Then
![]() $\sigma _0= {\mathrm {c-ind}}^{M^{\circ }}_{J_M} \lambda _M$
is an irreducible
$\sigma _0= {\mathrm {c-ind}}^{M^{\circ }}_{J_M} \lambda _M$
is an irreducible
![]() $M^{\circ }$
-summand of
$M^{\circ }$
-summand of
![]() $\sigma $
, and we have a canonical isomorphism (provided by induction in stages)
$\sigma $
, and we have a canonical isomorphism (provided by induction in stages)
Proof Using Frobenius reciprocity and Mackey theory (provided by [Reference Vignéras28, Section 5.5] in this setting), we get
 $$ \begin{align*} {\mathrm{Hom}}_{M^{\circ}}( \sigma_0, \sigma_0) &\cong {\mathrm{Hom}}_{M^{\circ}}\left({\mathrm{c-ind}}_{J_M}^{M^{\circ}} \lambda_M,{\mathrm{c-ind}}_{J_M}^{M^{\circ}} \lambda_M\right)\\ &\cong {\mathrm{Hom}}_{J_M}\left(\lambda_M,\bigoplus_x {\mathrm{c-ind}}_{J_M\cap {J_M^x}}^J \text{Res}_{J_M\cap {J_M^x}}^{J_M^x} \lambda_M^x\right), \end{align*} $$
$$ \begin{align*} {\mathrm{Hom}}_{M^{\circ}}( \sigma_0, \sigma_0) &\cong {\mathrm{Hom}}_{M^{\circ}}\left({\mathrm{c-ind}}_{J_M}^{M^{\circ}} \lambda_M,{\mathrm{c-ind}}_{J_M}^{M^{\circ}} \lambda_M\right)\\ &\cong {\mathrm{Hom}}_{J_M}\left(\lambda_M,\bigoplus_x {\mathrm{c-ind}}_{J_M\cap {J_M^x}}^J \text{Res}_{J_M\cap {J_M^x}}^{J_M^x} \lambda_M^x\right), \end{align*} $$
where the sum is taken over a set of double coset representatives in
![]() $J_M\backslash M^{\circ } /J_M$
. Fixing one such x, we see that
$J_M\backslash M^{\circ } /J_M$
. Fixing one such x, we see that
(here, we are using Frobenius reciprocity for a compact group, so that restriction is also a left adjoint for
![]() ${\mathrm {c-ind}}$
). Since only
${\mathrm {c-ind}}$
). Since only
![]() $x\in \tilde J_M$
intertwine
$x\in \tilde J_M$
intertwine
![]() $\lambda _M$
, and
$\lambda _M$
, and
![]() $J_M = \tilde J_M \cap M^{\circ }$
, we have
$J_M = \tilde J_M \cap M^{\circ }$
, we have
which we needed to prove.
Finally, we may put together the above results.
Proof According to (5.5) in [Reference Bushnell and Kutzko8], if M is a general linear group over a division algebra, then the conditions of the above lemma are satisfied for every irreducible cuspidal representation
![]() $\sigma $
of M. Clearly, if the conditions are satisfied for
$\sigma $
of M. Clearly, if the conditions are satisfied for
![]() $(M_1,\sigma _1)$
and
$(M_1,\sigma _1)$
and
![]() $(M_2,\sigma _2),$
then they are satisfied for
$(M_2,\sigma _2),$
then they are satisfied for
![]() $M=M_1\times M_2$
and
$M=M_1\times M_2$
and
![]() $\sigma =\sigma _1\otimes \sigma _2$
. Recall that a Levi subgroup in a classical group is a product of general linear groups and a smaller classical group. By a result of Stevens [Reference Stevens26], irreducible cuspidal representations of classical groups are induced from open compact subgroups if F has odd residue characteristic. Thus, in these cases, for every irreducible cuspidal representation
$\sigma =\sigma _1\otimes \sigma _2$
. Recall that a Levi subgroup in a classical group is a product of general linear groups and a smaller classical group. By a result of Stevens [Reference Stevens26], irreducible cuspidal representations of classical groups are induced from open compact subgroups if F has odd residue characteristic. Thus, in these cases, for every irreducible cuspidal representation
![]() $\sigma $
of M, there exists a type
$\sigma $
of M, there exists a type
![]() $(\tilde J_M, \tilde \lambda _M)$
satisfying the three bullets above, and Lemma A.4 applies. Moreover, by [Reference Bushnell and Kutzko7, Reference Stevens and Séchere27] (for general linear groups) and [Reference Miyauchi and Stevens21] (for classical groups), G admits a type
$(\tilde J_M, \tilde \lambda _M)$
satisfying the three bullets above, and Lemma A.4 applies. Moreover, by [Reference Bushnell and Kutzko7, Reference Stevens and Séchere27] (for general linear groups) and [Reference Miyauchi and Stevens21] (for classical groups), G admits a type
![]() $(J,\lambda )$
which is a cover of type
$(J,\lambda )$
which is a cover of type
![]() $(J_M,\lambda _M)$
, so we can apply Lemma A.3 to obtain an isomorphism of generators for
$(J_M,\lambda _M)$
, so we can apply Lemma A.3 to obtain an isomorphism of generators for
![]() $\mathrm {Rep}_{\mathfrak {s}}(G)$
.
$\mathrm {Rep}_{\mathfrak {s}}(G)$
.
This completes the proof of Theorem A.1.
We remark that Theorem A.1 holds beyond classical groups, provided that the conditions of two lemmas are satisfied. For exceptional
![]() $G_2$
examples, see [Reference Blondel5].
$G_2$
examples, see [Reference Blondel5].
Acknowledgment
We would like to thank K.-Y. Chan, Y. Sakellaridis, M. Solleveld, and S. Stevens for useful communications. We would also like to thank the Erwin Schrödinger Insitute in Vienna for providing a stimulating environment where this work was completed.