Article contents
Galois Theory of Essential Extensions of Modules
Published online by Cambridge University Press: 20 November 2018
Extract
The purpose of this paper is to exploit an analogy between algebraic extensions of fields and essential extensions of modules, in which the role of the algebraic closure of a field F is played by the injective hull H(M) of a unitary left R-module M. (The notion of * ‘algebraic’ extensions of general algebraic systems has been studied by Shoda; see, for example [5].)
In this analogy, the role of a polynomial p(x) is played by a homomorphism of R-modules
(1)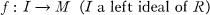
which will be called an ideal homomorphism into M. The process of solving the equation p(x) = 0 in F, or in an algebraic extension of F, will be replaced by the process of extending an ideal homomorphism (1) to a homomorphism F* from R into M, or into an essential extension of M.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1972
References
- 1
- Cited by


