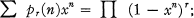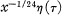Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Newman, Morris
1960.
Periodicity modulo 𝑚 and divisibility properties of the partition function.
Transactions of the American Mathematical Society,
Vol. 97,
Issue. 2,
p.
225.
Yaqub, Adil
Brauer, George
Khandekar, P. R.
Newman, Morris
Carlitz, L.
Bilodeau, G. G.
and
Burton, David M.
1964.
Mathematical Notes.
The American Mathematical Monthly,
Vol. 71,
Issue. 9,
p.
1010.
Newman, Morris
1967.
Note on partitions modulo 5.
Mathematics of Computation,
Vol. 21,
Issue. 99,
p.
481.
Atkin, A. O. L.
1967.
Proof of a conjecture of Ramanujan.
Glasgow Mathematical Journal,
Vol. 8,
Issue. 1,
p.
14.
Fomenko, O. M.
1980.
Applications of the theory of modular forms to number theory.
Journal of Soviet Mathematics,
Vol. 14,
Issue. 4,
p.
1307.
Newman, Morris
1990.
Analytic Number Theory.
p.
405.
Lovejoy, Jeremy
and
Ono, Ken
2002.
Extension of Ramanujan's congruences for the partition function modulo powers of 5.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2002,
Issue. 542,
BARUAH, NAYANDEEP DEKA
and
OJAH, KANAN KUMARI
2011.
SOME CONGRUENCES DEDUCIBLE FROM RAMANUJAN'S CUBIC CONTINUED FRACTION.
International Journal of Number Theory,
Vol. 07,
Issue. 05,
p.
1331.
JAMESON, MARIE
2012.
A REFINEMENT OF RAMANUJAN'S CONGRUENCES MODULO POWERS OF 7 AND 11.
International Journal of Number Theory,
Vol. 08,
Issue. 04,
p.
865.
de Azevedo Pribitkin, Wladimir
2016.
A generalization of Knopp’s Observation on Ramanujan’s tau-function.
The Ramanujan Journal,
Vol. 41,
Issue. 1-3,
p.
519.
Cui, Su-Ping
Gu, Nancy S.S.
and
Huang, Anthony X.
2016.
Congruence properties for a certain kind of partition functions.
Advances in Mathematics,
Vol. 290,
Issue. ,
p.
739.
Xia, Ernest X.W.
2020.
Newman's identities, lucas sequences and congruences for certain partition functions.
Proceedings of the Edinburgh Mathematical Society,
Vol. 63,
Issue. 3,
p.
709.
Zhou, Hai-Gang
and
Zhu, Xiao-Jie
2023.
Double coset operators and eta-quotients.
Journal of Number Theory,
Vol. 249,
Issue. ,
p.
537.
Du, Julia Q. D.
Lovejoy, Jeremy
and
Yao, Olivia
2024.
New congruences modulo 4 and 8 for Ramanujan’s 𝜙 function.
Proceedings of the American Mathematical Society,
Vol. 153,
Issue. 2,
p.
551.
Hu, Yueya
Liu, Eric H.
and
Yao, Olivia X. M.
2025.
Congruences modulo 4 and 8 for Ramanujan’s sixth-order mock theta function $$\rho (q)$$.
The Ramanujan Journal,
Vol. 66,
Issue. 4,
Talukdar, Pranjal
2025.
Density results and congruences for an analogue of t-core partitions.
The Ramanujan Journal,
Vol. 66,
Issue. 2,
Xia, Ernest X. W.
and
Xin, Liu Jin
2025.
The powers of Euler’s product and congruences for certain partition functions.
The Ramanujan Journal,
Vol. 67,
Issue. 1,