Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-25T20:09:11.822Z Has data issue: false hasContentIssue false
  • English
  • Français

A Further Generalization of an Irreducibility Theorem of A. Cohn

Published online by Cambridge University Press:  20 November 2018

Michael Filaseta
Michael Filaseta*
Affiliation:
University of Illinois, Urbana, Illinois
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let dndn–1 … d0 be the b-ary representation of a positive integer N. Call 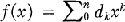the polynomial obtained from N base b. In the case the base is 10, f(x) will be called the polynomial obtained from N. Pólya and Szegö attribute the following theorem to A. Cohn [2, b. 2, VIII, 128]:

THEOREM 1. A polynomial obtained from a prime is irreducible.

This theorem was generalized in two different ways by John Brillhart, Andrew Odlyzko, and myself [1]. One way was by proving the theorem remains true regardless of the base being used. The second way was by permitting the coefficients of f(x) to be different from digits. Thus, for example, if 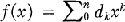, where 0 ≦ dk ≦ 167 for all k, and if f(10) is prime, then f(x) is irreducible. In this paper, Theorem 1 will be generalized in another way by considering composite N.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 34 , Issue 6 , 01 December 1982 , pp. 1390 - 1395
Copyright
Copyright © Canadian Mathematical Society 1982

References

1. Brillhart, J., Filaseta, M. and Odlyzko, A., On an irreducibility theorem of A. Cohn, Can. J. Math. 33 (1981).Google Scholar
2. Polya, G. and Szego, G., Aufgaben und Lehrsdtze aus der Analysis (Springer-Verlag, Berlin, 1964).Google Scholar