Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-05T05:08:39.478Z Has data issue: false hasContentIssue false
  • English
  • Français

Fundamental Group of Simple C*-algebras with Unique Trace III

Published online by Cambridge University Press:  20 November 2018

Norio Nawata
Norio Nawata*
Affiliation:
Graduate School of Mathematics, Kyushu University, Motooka, Fukuoka, 819-0395, Japan email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We introduce the fundamental group 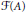$\mathcal{F}\left( A \right)$ of a simple $\sigma $-unital 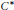${{C}^{*}}$–algebra 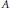$A$ with unique (up to scalar multiple) densely defined lower semicontinuous trace. This is a generalization of Fundamental Group of Simple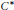${{C}^{*}}$-algebras with Unique Trace I and II by Nawata and Watatani. Our definition in this paper makes sense for stably projectionless 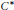${{C}^{*}}$-algebras. We show that there exist separable stably projectionless 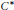${{C}^{*}}$-algebras such that their fundamental groups are equal to 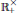$\mathbb{R}_{+}^{\times }$ by using the classification theorem of Razak and Tsang. This is a contrast to the unital case in Nawata and Watatani. This study is motivated by the work of Kishimoto and Kumjian.

Keywords

46L0546L0846L35fundamental groupPicard groupHilbert modulecountable basisstably projectionless algebradimension function
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 64 , Issue 3 , 01 June 2012 , pp. 573 - 587
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Blackadar, B., Operator algebras: Theory of C*-algebras and von Neumann algebras. Encyclopaedia of Mathematical Sciences, 122, Operator Algebras and Non-commutative Geometry, III, Springer-Verlag, Berlin, 2006.Google Scholar
[2] Blackadar, B. and Handelman, D., Dimension functions and traces on C*-algebras. J. Funct. Anal. 45(1982), no. 3, 297–340. http://dx.doi.org/10.1016/0022-1236(82)90009-X Google Scholar
[3] Blackadar, B. and Kumjian, A., Skew products of relations and the structure of simple C*-algebras. Math. Z. 189(1985), no. 1, 55–63. http://dx.doi.org/10.1007/BF01246943 Google Scholar
[4] Brown, L. G., Stable isomorphism of hereditary subalgebras of C*-algebras. Pacific J. Math. 71(1977), no. 2, 335–348.Google Scholar
[5] Brown, L. G., Green, P., and Rieffel, M. A., Stable isomorphism and strong Morita equivalence of C*-algebras. Pacific J. Math. 71(1977), no. 2, 349–363.Google Scholar
[6] Combes, F. and Zettl, H., Order structures, traces and weights on Morita equivalent C*-algebras. Math. Ann. 265(1983), no. 1, 67–81. http://dx.doi.org/10.1007/BF01456936 Google Scholar
[7] Connes, A., A factor of type II1 with countable fundamental group. J. Operator Theory 4(1980), no. 1, 151–153.Google Scholar
[8] Cuntz, J., Dimension functions on simple C*-algebras. Math. Ann. 233(1978), no. 2, 145–153. http://dx.doi.org/10.1007/BF01421922 Google Scholar
[9] Cuntz, J. and Pedersen, G. K., Equivalence and traces on C*-algebras. J. Funct. Anal. 33(1979), no. 2, 135–164. http://dx.doi.org/10.1016/0022-1236(79)90108-3 Google Scholar
[10] Elliott, G. A., An invariant for simple C*-algebras. Canadian Mathematical Society. 1945–1995, Vol. 3, Canadian Math. Soc., Ottawa, ON, 1996, pp. 61–90.Google Scholar
[11] Elliott, G. A. and Villadsen, J., Perforated ordered K0-groups. Canad. J. Math. 52(2000), no. 6, 1164–1191. http://dx.doi.org/10.4153/CJM-2000-049-9 Google Scholar
[12] Frank, M. and Larson, D., A module frame concept for Hilbert C*-modules. In: The functional and harmonic analysis of wavelets and frames (San Antonio, TX, 1999), Contemp. Math., 247, American Mathematical Society, Providence, RI, 1999, pp. 207–233.Google Scholar
[13] Frank, M. and Larson, D., Frames in Hilbert C*-modules and C*-algebras. J. Operator Theory 48(2002), no. 2, 273–314.Google Scholar
[14] Izumi, M., Kajiwara, T., and Watatani, Y., KMS states and branched points. Ergodic Theory Dynam. Systems 27(2007), no. 6, 1887–1918.Google Scholar
[15] Jacelon, B., A simple self-absorbing, stably projectionless C*-algebra. arxiv:1006.5397v1Google Scholar
[16] Kajiwara, T., Pinzari, C., and Watatani, Y., Ideal structure and simplicity of the C*-algebras generated by Hilbert bimodules. J. Funct. Anal. 159(1998), no. 2, 295–322. http://dx.doi.org/10.1006/jfan.1998.3306 Google Scholar
[17] Kajiwara, T., Jones index theory for Hilbert C*-bimodules and its equivalence with conjugation theory. J. Funct. Anal. 215(2004), no. 1, 1–49. http://dx.doi.org/10.1016/j.jfa.2003.09.008 Google Scholar
[18] Kajiwara, T. and Watatani, Y., Jones index theory by Hilbert C*-bimodules and K-theory. Trans. Amer. Math. Soc. 352(2000), no. 8, 3429–3472. http://dx.doi.org/10.1090/S0002-9947-00-02392-8 Google Scholar
[19] Kasparov, G. G., Hilbert C*-modules: theorems of Stinespring and Voiculescu. J. Operator Theory 4(1980), no. 1, 133–150.Google Scholar
[20] Kishimoto, A. and Kumjian, A., Simple stably projectionless C*-algebras arising as crossed products. Canad. J. Math. 48(1996), no. 5, 980–996. http://dx.doi.org/10.4153/CJM-1996-051-0 Google Scholar
[21] Kishimoto, A. and Kumjian, A., Crossed products of Cuntz algebras by quasi-free automorphisms. In: Operator algebras and their applications (Waterloo, ON, 1994/1995), Fields Inst. Commun., 13, American Mathematical Society, Providence, RI, 1997, pp. 173–192.Google Scholar
[22] Kodaka, K., Full projections, equivalence bimodules and automorphisms of stable algebras of unital C*-algebras. Operator Theory, J., 37(1997), no. 2, 357–369.Google Scholar
[23] Kodaka, K., Picard groups of irrational rotation C*-algebras. J. London Math. Soc. (2) 56(1997), no. 1, 179–188. http://dx.doi.org/10.1112/S0024610797005243 Google Scholar
[24] Kodaka, K., Projections inducing automorphisms of stable UHF-algebras. Glasg. Math. J. 41(1999), no. 3, 345–354. http://dx.doi.org/10.1017/S0017089599000336 Google Scholar
[25] Laca, M. and Neshveyev, S., KMS states of quasi-free dynamics on Pimsner algebras. J. Funct. Anal. 211(2004), no. 2, 457–482. http://dx.doi.org/10.1016/j.jfa.2003.08.008 Google Scholar
[26] Lance, E. C., Hilbert C*-modules. A toolkit for operator algebraists. London Mathematical Society Lecture Note Series, 210, Cambridge University Press, Cambridge, 1995.Google Scholar
[27] Manuilov, V. M. and Troitsky, E. V., Hilbert C*-modules. Translations of Mathematical Monographs, 226, American Mathematical Society, Providence, RI, 2005.Google Scholar
[28] Murray, F. J. and von Neumann, J., On rings of operators. IV. Ann. of Math. 44(1943), 716–808. http://dx.doi.org/10.2307/1969107 Google Scholar
[29] Nawata, N. and Watatani, Y., Fundamental group of simple C*-algebras with unique trace. Adv. Math. 225(2010), no. 1, 307–318. http://dx.doi.org/10.1016/j.aim.2010.02.019 Google Scholar
[30] Nawata, N. and Watatani, Y., Fundamental group of simple C*-algebras with unique trace II. J. Funct. Anal. 260(2011), no. 2, 428–435. http://dx.doi.org/10.1016/j.jfa.2010.09.014 Google Scholar
[31] Pedersen, G. K., Measure theory for C-algebras. III. Math. Scand. 25(1969), 71–93.Google Scholar
[32] Pedersen, G. K., C*-Algebras and their automorphism groups. London Mathematical Society Monographs, 14, Academic Press, London-New York, 1979.Google Scholar
[33] Pinzari, C., Watatani, Y., and Yonetani, K., KMS states, entropy and the variational principle in full C*-dynamical systems. Comm. Math. Phys. 213(2000), no. 2, 331–379. http://dx.doi.org/10.1007/s002200000244 Google Scholar
[34] Popa, S., Strong rigidity of II1 factors arising from malleable actions of w-rigid groups. I. Invent. Math. 165(2006), no. 2, 369–408. http://dx.doi.org/10.1007/s00222-006-0501-4 Google Scholar
[35] Popa, S. and Vaes, S., Actions of F1 whose II1 factors and orbit equivalence relations have prescribed fundamental group. J. Amer. Math. Soc. 23(2010), no. 2, 383–403. http://dx.doi.org/10.1090/S0894-0347-09-00644-4 Google Scholar
[36] Řadulescu, F., The fundamental group of the von Neumann algebra of a free group with infinitely many generators is R_ +. J. Amer. Math. Soc. 5(1992), no. 3, 517–532.Google Scholar
[37] Razak, S., On the classification of simple stably projectionless C*-algebras. Canad. J. Math. 54(2002), no. 1, 138–224. http://dx.doi.org/10.4153/CJM-2002-006-7 Google Scholar
[38] Raeburn, I. and D. P.Williams, Morita equivalence and continuous-trace C*-algebras. Mathematical Surveys and Monographs, 60, American Mathematical Society, Providence, RI, 1998.Google Scholar
[39] Rieffel, M. A., Morita equivalence for operator algebras. In: Operator algebras and applications, Part I (Kingston, Ont., 1980), Proc. Sympos. Pure Math., 38, American Mathematical Society, Providence, RI, 1982, pp. 285–298.Google Scholar
[40] Tsang, K.-W., On the positive tracial cones of simple stably projectionless C*-algebras. J. Funct. Anal. 227(2005), no. 1, 188–199. http://dx.doi.org/10.1016/j.jfa.2005.01.007 Google Scholar
[41] Voiculescu, D., Circular and semicircular systems and free product factors. In: Operator algebras, unitary representations, enveloping algebras, and invariant theory (Paris, 1989), Progr. Math. 92, Birkhäuser Boston, Boston, MA, 1990, pp. 45–60.Google Scholar
[42] Watatani, Y., Index for C*-subalgebras. Mem. Amer. Math. Soc. 83(1990), no. 424.Google Scholar