Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T00:38:14.433Z Has data issue: false hasContentIssue false
  • English
  • Français

Fundamental Biorthogonal Sequences and K-Norms on ϕ

Published online by Cambridge University Press:  20 November 2018

L. Crone ,
D. J. Fleming  and
P. Jessup
L. Crone
Affiliation:
Clarkson College of Technology, Potsdam, New York
D. J. Fleming
Affiliation:
Clarkson College of Technology, Potsdam, New York
P. Jessup
Affiliation:
Clarkson College of Technology, Potsdam, New York
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A biorthogonal sequence is a double sequence (xi,fi) where each xi is from some locally convex space X, each fi is from X* and fi(xj) = δij. A biorthogonal sequence is called total if the functionals (fi) are total over X and is called fundamental if sp(xi) is dense in X. If a biorthogonal sequence is both total and fundamental we refer to it as a Markushivich basis or, more simply, an M-basis.

If (xi,fi) is a total biorthogonal sequence for X, then X can be identified with the space of all scalar sequences (fi(x)) under the correspondence x ↔ (fi(x)). We refer to this space as the associated sequence space with respect to (xi, fi). With this correspondence, xi corresponds to 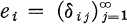and fi corresponds to Ei, the ith coordinate functional.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 23 , Issue 6 , December 1971 , pp. 1040 - 1050
Copyright
Copyright © Canadian Mathematical Society 1971

References

1. Day, M. M., Normed linear spaces (Springer-Verlag, Berlin-Gottingen-Heidelberg, 1962).Google Scholar
2. Gaposhkin, V. F. and Kadets, M. I., Operator bases in Banach spaces, (Russian) Mat. Sb. (N.S.) 61 (103) (1963), 3–12.Google Scholar
3. McGivney, R. J. and Ruckle, W., Multiplier algebras of biorthogonal systems, Pacific J. Math. 29 (1969), 375–387.Google Scholar
4. Ruckle, W., Lattices of sequence spaces, Duke Math. J. 35 (1968), 491–504.Google Scholar
5. Ruckle, W., Representation and series summability of complete biorthogonal sequences, Pacific J. Math. 34 (1970), 509–526.Google Scholar
6. Wilansky, A., Functional analysis (Blaisdell, New York, 1964).Google Scholar
7. Yamazaki, S., Normed rings and unconditional bases in Banach spaces, Sci. Papers College Gen. Ed. Univ. Tokyo. 14 (1964), 1–10.Google Scholar
8. Yamazaki, S., Normed rings and bases in Banach spaces, Sci. Papers College Gen. Ed. Univ. Tokyo. 15 (1965), 1–13.Google Scholar