Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-05T11:46:36.712Z Has data issue: false hasContentIssue false
  • English
  • Français

Functoriality of the Canonical Fractional Galois Ideal

Published online by Cambridge University Press:  20 November 2018

Paul Buckingham  and
Victor Snaith
Paul Buckingham*
Affiliation:
Department of Mathematical and Statistical Sciences, University of Alberta, Edmonton, AB
Victor Snaith*
Affiliation:
School of Mathematics and Statistics, The University of Sheffield, Western Bank, Sheffield, UK
*
[email protected]
[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The fractional Galois ideal is a conjectural improvement on the higher Stickelberger ideals defined at negative integers, and is expected to provide non-trivial annihilators for higher 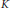$K$-groups of rings of integers of number fields. In this article, we extend the definition of the fractional Galois ideal to arbitrary (possibly infinite and non-abelian) Galois extensions of number fields under the assumption of Stark's conjectures and prove naturality properties under canonical changes of extension. We discuss applications of this to the construction of ideals in non-commutative Iwasawa algebras.

Keywords

11R4211R2311R70
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 62 , Issue 5 , 01 October 2010 , pp. 1011 - 1036
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Ardakov, K. and Brown, K. A., Ring-theoretic properties of Iwasawa algebras: a survey. Doc. Math. 2006, (Extra Vol.), 7–33.Google Scholar
[2] Ardakov, K. and Brown, K. A., Primeness, semiprimeness and localisation in Iwasawa algebras. Trans. Amer. Math. Soc. 359(2007), no. 4, 1499–1515. doi:10.1090/S0002-9947-06-04153-5Google Scholar
[3] Ardakov, K., F.Wei, and Zhang, J. J., Reflexive ideals in Iwasawa algebras. Adv. Math. 218(2008), no. 3, 865–901. doi:10.1016/j.aim.2008.02.004Google Scholar
[4] Brumer, A., On the units of algebraic number fields. Mathematika 14(1967), 121–124. doi:10.1112/S0025579300003703Google Scholar
[5] Buckingham, P., The canonical fractional Galois ideal at s = 0. J. Number Theory 128(2008), no. 6, 1749–1768. doi:10.1016/j.jnt.2007.09.001Google Scholar
[6] Buckingham, P., The canonical fractional Galois ideal at s = 0. Ph. D. thesis, University of Sheffield, 2008. doi:10.1016/j.jnt.2007.09.001Google Scholar
[7] Burns, D., On leading terms and values of equivariant motivic L-functions. Pure Appl. Math. Q. 6(2010), no. 1, 83–172.Google Scholar
[8] Cassou-Noguès, P., Valeurs aux entiers négatifs des fonctions zêta et fonctions zêta p-adiques. Invent. Math. 51(1979), no. 1, 29–59. doi:10.1007/BF01389911Google Scholar
[9] Coates and W, J.. Sinnott, On p-adic L-functions over real quadratic fields. Invent. Math. 25(1974), 253–279. doi:10.1007/BF01389730Google Scholar
[10] Coates, J., Fragments of the GL2 Iwasawa theory of elliptic curves without complex multiplication. In: Arithmetic theory of elliptic curves (Cetraro, 1997), Lecture Notes in Math., 1716, Springer, Berlin, 1999, pp. 1–50. doi:10.1007/BFb0093452Google Scholar
[11] Coates, J., Fukaya, T., Kato, K., Sujatha, R., and Venjakob, O., The GL2 main conjecture for elliptic curves without complex multiplication. Publ. Math. Inst. Hautes Études Sci. 101(2005), 163–208. doi:10.1007/s10240-004-0029-3Google Scholar
[12] Coates and W, J.. Sinnott, An analogue of Stickelberger's theorem for the higher K-groups. Invent. Math. 24(1974), 149–161. doi:10.1007/BF01404303Google Scholar
[13] Cornacchia, P. and Greither, C., Fitting ideals of class groups of real fields with prime power conductor. Number Theory, J., 73(1998), no. 2, 459–471. doi:10.1006/jnth.1998.2300Google Scholar
[14] Deligne, P. and Ribet, K. A., Values of abelian L-functions at negative integers over totally real fields. Invent. Math. 59(1980), no. 3, 227–286. doi:10.1007/BF01453237Google Scholar
[15] Fukaya, T. and Kato, K., A formulation of conjectures on p-adic zeta functions in noncommutative Iwasawa theory. In: Proceedings of the St. Petersburg Mathematical Society, XII, Amer. Math. Soc. Transl. Ser. 2, 219, American Mathematical Society, Providence, RI, 2006, pp. 1–85.Google Scholar
[16] Gross, B. H., On the values of Artin L-functions. Q. J. Pure Appl. Math 1(2005), no. 1, 1-13.Google Scholar
[17] Hachimori, Y. and Sharifi, R. T., On the failure of pseudo-nullity of Iwasawa modules. J. Algebraic Geom. 14(2005), no. 3, 567–591.Google Scholar
[18] Hayes, D. R., Stickelberger functions for non-abelian Galois extensions of global fields. In: Stark’s conjectures: recent work and new directions, Contemp. Math., 358, American Mathematical Society, Providence, RI, y, pp. 193–206.Google Scholar
[19] Iwasawa, K., Lectures on p-adic L-functions. Annals of Mathematics Studies, 74, Princeton University Press, Princeton, NJ, 1972.Google Scholar
[20] Kubota, T. and Leopoldt, H.-W., Eine p-adische Theorie der Zetawerte. I. Einführung der p-adischen Dirichletschen L-Funktionen. J. Reine Angew. Math. 214/215(1964), 328–339.Google Scholar
[21] Lang, S., Algebra. Second ed., Addison-Wesley Publishing Company Advanced Book Program, Reading, MA, 1984.Google Scholar
[22] Martinet, J., Character theory and Artin L-functions. In: Algebraic number fields: L-functions and Galois properties (Proc. Sympos., Univ. Durham, Durham, 1975), Academic Press, London, 1977, pp. 1–87.Google Scholar
[23] Mazur, B. and Wiles, A., Class fields of abelian extensions of Q. Invent. Math. 76(1984), no. 2, 179–330. doi:10.1007/BF01388599Google Scholar
[24] Popescu, C. D., Rubin's integral refinement of the abelian Stark conjecture. In: Stark's conjectures: recent work and new directions, Contemp. Math., 358, American Mathematical Society, Providence, RI, 2004, pp. 1–35.Google Scholar
[25] Quillen, D., Higher algebraic K-theory. I. In: Algebraic K-theory, I: Higher K-theories (Proc. Conf., Battelle Memorial Inst., Seattle,Wash., 1972), Lecture Notes in Math., 341, Springer, Berlin, 1973, pp. 85–147.Google Scholar
[26] Ritter, J. and Weiss, A., Toward equivariant Iwasawa theory. I. Manuscripta Math. 109(2002), no. 2, 131–146, doi:10.1007/s00229-002-0306-8; Part II, Indag. Math. (N.S.) 15(2004), no. 4, 549–572, doi:10.1007/s00208-006-0773-4; Part III, Math. Ann. 336(2006), no. 1, 27–49, doi:10.1007/s00208-006-0773-4; Part IV, Homology, Homotopy Appl. 7(2005), no. 3, 155–171.Google Scholar
[27] Ritter, J. and Weiss, A., The lifted root number conjecture and Iwasawa theory. Mem. Amer. Math. Soc. 157(2002), no. 748.Google Scholar
[28] Rubin, K., Stark units and Kolyvagin's “Euler systems”. J. Reine Angew. Math. 425(1992). 141–154. doi:10.1515/crll.1992.425.141Google Scholar
[29] Serre, J.-P., Linear representations of finite groups. Graduate Texts in Mathematics, 42, Springer-Verlag, New York, 1977.Google Scholar
[30] Snaith, V., Equivariant motivic phenomena. In: Axiomatic, enriched and motivic homotopy theory, NATO Sci. Ser. II Math. Phys. Chem., 131, Kluwer Acad. Publ., Dordrecht, 2004, pp. 335–383.Google Scholar
[31] Snaith, V., Explicit Brauer induction.With applications to algebra and number theory. Cambridge Studies in Advanced Mathematics, 40, Cambridge University Press, Cambridge, 1994.Google Scholar
[32] Snaith, V., Relative K0, annihilators, Fitting ideals and Stickelberger phenomena. Proc. London Math. Soc. (3) 90(2005), no. 3, 545–590. doi:10.1112/S0024611504015163Google Scholar
[33] Snaith, V., Stark's conjecture and new Stickelberger phenomena. Canad. J. Math. 58(2006), no. 2, 419–448.Google Scholar
[34] Stopple, J., Stark conjectures for C M elliptic curves over number fields. J. Number Theory 103(2003), no. 2, 163–196. doi:10.1016/S0022-314X(03)00112-4Google Scholar
[35] Tate, J., Les conjectures de Stark sur les fonctions L d’Artin en s = 0. Lecture notes edited by Dominique Bernardi and Norbert Schappacher. Progress in Mathematics, 47, Birkhäuser Boston Inc., Boston, MA, 1984.Google Scholar
[36] Venjakob, O., On the structure theory of the Iwasawa algebra of a p-adic Lie group. J. Eur. Math. Soc. 4(2002), no. 3, 271–311. doi:10.1007/s100970100038Google Scholar
[37] Venjakob, O., A non-commutative Weierstrass preparation theorem and applications to Iwasawa theory. J. Reine Angew. Math. 559(2003), 153–191. doi:10.1515/crll.2003.047Google Scholar
[38] Venjakob, O., On the Iwasawa theory of p-adic Lie extensions. Compositio Math. 138(2003), no. 1, 1–54. doi=10.1023/A:1025413030203 doi:10.1023/A:1025413030203Google Scholar
[39] Washington, L. C., Introduction to cyclotomic fields. Second ed., Graduate Texts in Mathematics, 83, Springer-Verlag, New York, 1997.Google Scholar
[40] Wiles, A., The Iwasawa conjecture for totally real fields. Ann. of Math. 131(1990), no. 3, 493–540. doi=10.2307/1971468 doi:10.2307/1971468Google Scholar