Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T19:01:30.608Z Has data issue: false hasContentIssue false
  • English
  • Français

Functional Equations, Distributions and Approximate Identities

Published online by Cambridge University Press:  20 November 2018

John A. Baker
John A. Baker*
Affiliation:
University of Waterloo, Waterloo, OntarioCanada N2L 3G1
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The subject of this paper is the use of the theory of Schwartz distributions and approximate identities in studying the functional equation

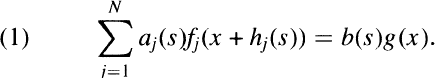
The aj’s and b are complex-valued functions defined on a neighbourhood, U, of 0 in Rm, hj. U → Rn with hj(0) = 0 and fj, g: Rn → C for 1 ≦ j ≦ N. In most of what follows the aj's and hj's are assumed smooth and may be thought of as given. The fj‘s, b and g may be thought of as the unknowns. Typically we are concerned with locally integrable functions f1, … , fN such that, for each s in U, (1) holds for a.e. (almost every) x ∈ Rn, in the sense of Lebesgue measure.

Keywords

39B2039B3039B4046F99
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 42 , Issue 4 , 01 August 1990 , pp. 696 - 708
Copyright
Copyright © Canadian Mathematical Society 1990

References

1. Aczél, J., Lectures on functional equations and their applications, Academic Press, New York- London, 1966.Google Scholar
2. Aczél, J., Haruki, H., McKiernan, M.A. and Sakovic, G.N., General and regular solutions offunctional equations characterizing harmonic polynomials, Aequationes Math. 1 (1968), 37–53.Google Scholar
3. Baker, John A., An Analogue of The Wave Equation and Certain Related Functional Equations,, Canad. Math. Bull., 12, No. 6 (1969), 837–846.Google Scholar
4. Baker, John A., Functional Equations, Tempered Distributions and Fourier Transforms, Trans Amer. Math. Soc. 315, Sept. 1989, 57–68.Google Scholar
5. Fejér, L., Untersuchungen iiber Fouriersche Reihen, Math. Ann. LVIII (1904), 51–69.Google Scholar
6. Gilbarg, D., and Trudinger, N.S., Elliptic Partial Differential Equations of Second Order, 2nd Edn., Springer Verlag, Berlin, Heidelberg, New York, Tokyo, 1983.Google Scholar
7. Katznelson, Yitzhak, An Introduction to Harmonic Analysis, Dover, New York, 1976.Google Scholar
8. Kemperman, J.H.B., A general functional equation, Trans. Amer. Math. Soc. 86 (1957), 28–56.Google Scholar
9. McKiernan, M.A., Boundedness on a set of Positive Measure and the Mean Value PropertyCharacterizes Polynomials on a Space Vn , Aequationes Math. 4 (1970), 31–36.Google Scholar
10. Rudin, Walter. Functional Analysis, McGraw-Hill, New York, 1973.Google Scholar
11. Scheinberg, Stephen, Uniform approximation by entire functions., Journal d'Analyse Mathématique 29 (1976), 16–19.Google Scholar
12. Swiatak, H., On the regularity of the distributional and continuous solutions of the functionalEquations, Aequationes Math. l (1968), 6–19.Google Scholar
13. Weierstrass, Karl, Math. Werke, Bd, III, Berlin: Mayer u. Muller, 1903, 1–37.Google Scholar