Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-22T14:18:06.975Z Has data issue: false hasContentIssue false
  • English
  • Français

Frobenius Algebras and Their Quivers

Published online by Cambridge University Press:  20 November 2018

Edward L. Green
Edward L. Green*
Affiliation:
Virginia Polytechnic Institute and State University, Blacksburg, Virginia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper studies the construction of Frobenius algebras. We begin with a description of when a graded 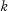-algebra has a Frobenius algebra as a homomorphic image. We then turn to the question of actual constructions of Frobenius algebras. We give a, method for constructing Frobenius algebras as factor rings of special tensor algebras. Since the representation theory of special tensor algebras has been studied intensively ([6], see also [2; 3; 4]), our results permit the construction of Frobenius algebras which have representations with prescribed properties. Such constructions were successfully used in [9].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 30 , Issue 5 , 01 October 1978 , pp. 1029 - 1044
Copyright
Copyright © Canadian Mathematical Society 1978

References

1. Curtis, C. and Reiner, I., Representation theory of finite groups and associative algebras Interscience Publishers, New York, London, Sydney, 1962).Google Scholar
2. Dlab, V. and Ringel, C., On algebras of finite representation type, J. of Alg. 33 (1975), 306–394.Google Scholar
3. Dlab, V. and Ringel, C., Indecomposable representations of graphs and algebras, Memoirs of the Am. Math. Soc. 173 (6) (1976), 1–57.Google Scholar
4. Gabriel, P., Indecomposable representations II, Symposia Mathematica, Instituto naxional di alta mathematica, 11 (1973), 81–104.Google Scholar
5. Gordon, R. and Green, E. L., Modules with cores and amalgamations of indecomposable modules, Memoirs of the Am. Math. Soc. 187 (10) (1977), 1–145.Google Scholar
6. Green, E. L., Representation theory of tensor algebras, J. of Alg. 34 (1975), 136–171.Google Scholar
7. Green, E. L., Gorenstein ideals and complete intersections, J. of Alg. 52 (1978), 264–273.Google Scholar
8. Green, E. L. and Reiten, I., On the construction of ring extensions, Glasgow Math. J. 17 (1976), 1–11.Google Scholar
9. Gustafson, W. and Green, E. L., Pathological Q — F algebras of finite type, Comm. in Alg. 2 (1974), 233–266.Google Scholar
10. Nakayama, T., On Frobeniusean algebras II, Ann. of Math. 42 (1941), 1–21.Google Scholar
11. Muller, W., Unzelegbare Muduln uber artinschen Ringen, Math. Zeitschr. 137 (1974), 197–226.Google Scholar