Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Auinger, Karl
1993.
The word problem for the bifree combinatorial strict regular semigroup.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 113,
Issue. 3,
p.
519.
Auinger, Karl
1993.
Bifree objects in e-varieties of strict orthodox semigroups and the lattice of strict orthodox *-semigroup varieties.
Glasgow Mathematical Journal,
Vol. 35,
Issue. 1,
p.
25.
Cherubini, Alessandra
Meakin, John
and
Piochi, Brunetto
1997.
Amalgams of free inverse semigroups.
Semigroup Forum,
Vol. 54,
Issue. 1,
p.
199.
Teixeira, M.Lurdes
2001.
On semidirectly closed pseudovarieties of aperiodic semigroups.
Journal of Pure and Applied Algebra,
Vol. 160,
Issue. 2-3,
p.
229.
Kad'ourek, Jiří
2003.
Finite orthodox locally idempotent semigroups having no finite basis of biidentities.
Journal of Algebra,
Vol. 266,
Issue. 2,
p.
446.
SEIF, STEVE
2005.
THE PERKINS SEMIGROUP HAS CO-NP-COMPLETE TERM-EQUIVALENCE PROBLEM.
International Journal of Algebra and Computation,
Vol. 15,
Issue. 02,
p.
317.
Lawson, Mark V.
Margolis, Stuart W.
and
Steinberg, Benjamin
2006.
Expansions of inverse semigroups.
Journal of the Australian Mathematical Society,
Vol. 80,
Issue. 2,
p.
205.
Kitaev, Sergey
and
Seif, Steve
2008.
Word Problem of the Perkins Semigroup via Directed Acyclic Graphs.
Order,
Vol. 25,
Issue. 3,
p.
177.
Myasnikov, A.
Roman’kov, V.
Ushakov, A.
and
Vershik, A.
2010.
The word and geodesic problems in free solvable groups.
Transactions of the American Mathematical Society,
Vol. 362,
Issue. 9,
p.
4655.
Margolis, Stuart
2021.
A tribute to John Meakin on the occasion of his 75th birthday.
Semigroup Forum,
Vol. 102,
Issue. 1,
p.
1.
Nyberg-Brodda, Carl-Fredrik
2022.
On one-relator groups and units of special one-relation inverse monoids.
International Journal of Algebra and Computation,
Vol. 32,
Issue. 07,
p.
1379.
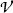 ∨
∨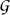 where
where 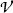 is a variety of inverse semigroups and
is a variety of inverse semigroups and 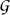 is the variety of groups.
is the variety of groups.

