Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T00:32:25.387Z Has data issue: false hasContentIssue false
  • English
  • Français

Free Involutorial Completely Simple Semigroups

Published online by Cambridge University Press:  20 November 2018

J. A. Gerhard  and
Mario Petrich
J. A. Gerhard
Affiliation:
University of Manitoba, Winnipeg, Manitoba
Mario Petrich
Affiliation:
University of Manitoba, Winnipeg, Manitoba
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An involution x → x* of a semigroup S is an antiautomorphism of S of order at most 2, that is (xy)* = y*x* and x** = x for all x, y ∊ S. In such a case, S is called an involutorial semigroup if regarded as a universal algebra with the binary operation of multiplication and the unary operation *. If S is also a completely simple semigroup, regarded as an algebra with multiplication and the unary operation x → x−1 of inversion (x−1 is the inverse of x in the maximal subgroup of S containing x), then (S, −1, *), or simply S, is an involutorial completely simple semigroup. All such S form a variety determined by the identities above concerning * and

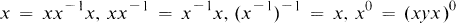
where x0 = xx−1.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 37 , Issue 2 , 01 April 1985 , pp. 271 - 295
Copyright
Copyright © Canadian Mathematical Society 1985

References

1. Clifford, A. H., The free completely regular semigroup on a set, J. Algebra 59 (1979), 434–451.Google Scholar
2. Clifford, A. H. and Preston, G. B., The algebraic theory of semigroups, Vol. I (Amer. Math. Soc, Providence, 1961).Google Scholar
3. Gerhard, J. A. and Petrich, M., Word problems for free objects in certain varieties of completely regular semigroups, Pacific J. Math. 104 (1983), 351–359.Google Scholar
4. Jones, P. R., Completely simple semigroups: free products, free semigroups and varieties, Proc. Roy. Soc. Edinburgh 88A (1981), 293–313.Google Scholar
5. Nordahl, T. E. and Scheiblich, H. E., Regular *-Semigroups, Semigroup Forum 16 (1978), 368–377.Google Scholar
6. Petrich, M., Certain varieties of completely regular *-semigroups. Boll. Unione Mat. Italiana (to appear).CrossRefGoogle Scholar
7. Rasin, V. V., Free completely simple semigroups, Matem. Zapiski Ural. Univ. 11 (1979). 140–151 (Russian).Google Scholar
8. Wagner, V. V., Generalized heaps and generalized groups with a transitive compatibility relation, Uč. zap. Saratov, univ., meh.-matem. 70 (1961), 25–39 (Russian).Google Scholar