Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T01:21:37.046Z Has data issue: false hasContentIssue false
  • English
  • Français

Frames and Stable Bases for Shift-Invariant Subspaces of L2(ℝd)

Published online by Cambridge University Press:  20 November 2018

Amos Ron  and
Zuowei Shen
Amos Ron
Affiliation:
Computer Science Department, University of Wisconsin-Madison, 1210 West Dayton Street, Madison, Wisconsin 53706, U.S.A. e-mail: [email protected]
Zuowei Shen
Affiliation:
Department of Mathematics, National University of Singapore, 10 Kent Ridge Crescent, Singapore 0511 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

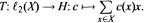Let X be a countable fundamental set in a Hilbert space H, and let T be the operator Whenever T is well-defined and bounded, X is said to be a Bessel sequence. If, in addition, ran T is closed, then X is a frame. Finally, a frame whose corresponding T is injective is a stable basis (also known as a Riesz basis). This paper considers the above three properties for subspaces H of L2(ℝd), and for sets X of the form 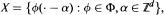with Φ either a singleton, a finite set, or, more generally, a countable set. The analysis is performed on the Fourier domain, where the two operators TT* and T* T are decomposed into a collection of simpler "fiber" operators. The main theme of the entire analysis is the characterization of each of the above three properties in terms of the analogous property of these simpler operators.

Keywords

42C15Riesz basesstable basesshift-invariant basesPSI spacesFSI spacesframesBessel sequenceswaveletssplines
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 47 , Issue 5 , 01 October 1995 , pp. 1051 - 1094
Copyright
Copyright © Canadian Mathematical Society 1995

References

[BDRl] de Boor, C., DeVore, R. and Ron, A., The structure of finitely generated shift-invariant spaces in L,2(ℝd),, J. Funct. Anal. 119(1994), 37–78.Google Scholar
[BDR2] de Boor, C., Approximation from shift-invariant subspaces of L2(ℝd), Trans. Amer. Math. Soc. 341(1994), 787–80.Google Scholar
[BL] Benedetto, J.J. and Li, S., The theory of multiresolution analysis frames and applications to filter design, preprint, 1994 Google Scholar
[BW] Benedetto, John J. and David Walnut, F., Gabor frames for L2 and related spaces, In: Wavelets: Mathematics and Applications, (eds. Benedetto, J. and Frazier, M.), CRC Press, Boca Raton, Florida, 1994. 97–162.Google Scholar
[C] Chui, C.K., An introduction to wavelets, Academic Press, Boston, 1992.Google Scholar
[Dl] Daubechies, I., The wavelet transform, time-frequency localization and signal analysis, IEEE Trans. Inform. Theory 36(1990), 961–1005.Google Scholar
[D2] Daubechies, I., Ten lectures on wavelets, CBMS-NSF Regional Conf. Ser. in Appl. Math. 61, SIAM, Philadelphia, 1992.Google Scholar
[DS] Duffin, R.J. and Schaeffer, A.C., A class of nonharmonic Fourier series, Trans. Amer. Math. Soc. 72(1952), 147–158.Google Scholar
[HW] Heil, C. and Walnut, D., Continuous and discrete wavelet transforms, SIAM Rev. 31(1989), 62S-666.Google Scholar
[JM] Jia, R.Q. and Micchelli, C.A., Using the refinement equation for the construction of pre-wavelets II: Powers of two, In: Curves and Surfaces, (eds. Laurent, P.J., Le, A. Mëhautë, and Schumaker, L.L.), Academic Press, New York, 1990. 209–246.Google Scholar
[JS] Jia, R.Q. and Shen, Z., Multiresolution and wavelets, Proc. Edinburgh Math. Soc, to appear.Google Scholar
[RSI] Ron, A. and Shen, Z., Weyl-Heisenberg frames and stable bases, CMS TSR 95-03, University of Wisconsin-Madison, October, 1994. Ftp site ftp.cs.wise.edu,file Approx/wh.ps.Google Scholar
[RS2] Ron, A., Affineframes and stable bases, manuscript, (1995).Google Scholar
[Ru] Rudin, W., Functional analysis, McGraw-Hill, New York, 1973.Google Scholar