Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T01:03:16.537Z Has data issue: false hasContentIssue false
  • English
  • Français

Fractional Derivatives as Inverses

Published online by Cambridge University Press:  20 November 2018

Godfrey L. Isaacs
Godfrey L. Isaacs*
Affiliation:
Lehman College, City University of New York, Bronx, New York
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We write formally (C, p) indicating that the integral is summable (C, p), i.e.,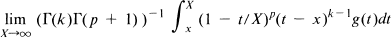if this limit exists. We note here that all integrals over a finite range are taken in the Lebesgue sense, and all inversions of such iterated integrals are justifiable by Fubini's Theorem.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 41 , Issue 1 , 01 February 1989 , pp. 178 - 192
Copyright
Copyright © Canadian Mathematical Society 1989

References

1. Andersen, A.F., Summation af ikke hel Orden, Mat. Tidsskrift, B (1946), 33–52.Google Scholar
2. Borwein, D., A summability factor theorem, J. London Math. Soc. 25 (1950), 302–315.Google Scholar
3. Bosanquet, L.S., On Liouville's extension of Abel's integral equation, Mathematika 16 (1969), 59–65.Google Scholar
4. Cossar, J., A theorem on Cesàro summability, J. London Math. Soc. 16 (1941), 56–68.Google Scholar
5. Isaacs, G.L., The iteration formula for inverted fractional integrals, Proc. London Math. Soc. (3) (1961), 213–238.Google Scholar
6. Isaacs, G.L., An iteration formula for fractional differences, Proc. London Math. Soc. (3. 13 (1963), 430–460.Google Scholar
7. Isaacs, G.L., Exponential laws for fractional differences, Math. Comp. 35 (1980), 933–936.Google Scholar
8. Whittaker, E.T. and Watson, G. N., A course of modern analysis (Cambridge University Press, London, 1940).Google Scholar