A reverse iterated function system (r.i.f.s.) is defined to be a set of expansive maps $\left\{ {{T}_{1}},...,{{T}_{m}} \right\}$ on a discrete metric space 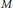$M$. An invariant set $F$ is defined to be a set satisfying 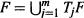$F\,=\,\bigcup _{j=1}^{m}\,{{T}_{j}}F$, and an invariant measure 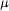$\mu $ is defined to be a solution of 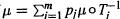$\mu \,=\,\sum{_{j=1}^{m}\,{{p}_{j}}\mu {}^\circ T_{j}^{-1}}$ for positive weights 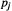${{p}_{j}}$. The structure and basic properties of such invariant sets and measures is described, and some examples are given. A blowup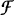$\mathcal{F}$ of a self-similar set $F$ in 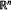${{\mathbb{R}}^{n}}$ is defined to be the union of an increasing sequence of sets, each similar to $F$. We give a general construction of blowups, and show that under certain hypotheses a blowup is the sum set of $F$ with an invariant set for a r.i.f.s. Some examples of blowups of familiar fractals are described. If 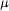$\mu $ is an invariant measure on 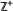${{\mathbb{Z}}^{+}}$ for a linear r.i.f.s., we describe the behavior of its analytic transform, the power series 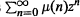$\sum{_{n=0}^{\infty }\mu (n){{z}^{n}}}$ on the unit disc.