Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T09:22:11.726Z Has data issue: false hasContentIssue false
  • English
  • Français

A Fractal Function Related to the John–Nirenberg Inequality for Qα(ℝn)

Published online by Cambridge University Press:  20 November 2018

Hong Yue
Hong Yue*
Affiliation:
Trine University, Angola, IN, U.S.A.
*
[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

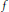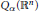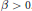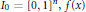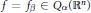A borderline case function $f$ for ${{Q}_{\alpha }}\left( {{\mathbb{R}}^{n}} \right)$ spaces is defined as a Haar wavelet decomposition, with the coefficients depending on a fixed parameter $\beta \,>\,0$. On its support ${{I}_{0}}\,=\,{{\left[ 0,\,1 \right]}^{n}},\,f\left( x \right)$ can be expressed by the binary expansions of the coordinates of $x$. In particular, $f\,=\,{{f}_{\beta }}\,\in \,{{Q}_{\alpha }}\left( {{\mathbb{R}}^{n}} \right)$ if and only if 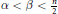$\alpha \,<\,\beta \,<\frac{n}{2}$ , while for 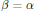$\beta \,=\,\alpha $, it was shown by Yue and Dafni that $f$ satisfies a John–Nirenberg inequality for 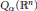${{Q}_{\alpha }}\left( {{\mathbb{R}}^{n}} \right)$. When 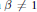$\beta \,\ne \,1$, 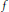$f$ is a self-affine function. It is continuous almost everywhere and discontinuous at all dyadic points inside 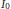${{I}_{0}}$. In addition, it is not monotone along any coordinate direction in any small cube. When the parameter 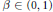$\beta \,\in \,\left( 0,\,1 \right)$, 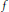$f$ is onto from 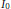${{I}_{0}}$ to 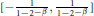$\left[ -\frac{1}{1-{{2}^{-\beta }}},\,\frac{1}{1-{{2}^{-\beta }}} \right]$ , and the graph of 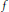$f$ has a non-integer fractal dimension 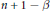$n\,+\,1\,-\beta$.

Keywords

42B3542C1030D5028A80Haar waveletsQ spacesJohn–Nirenberg inequalityGreedy expansionself-affinefractalBox dimension
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 62 , Issue 5 , 01 October 2010 , pp. 1182 - 1200
Copyright
Copyright © Canadian Mathematical Society 2010

Footnotes

Supported in part by NSERC and the CRM, Montréal.

References

[1] Chang, D-C. and Sadosky, C., Functions of bounded mean oscillation. Taiwanese J. Math. 10(2006), no. 3, 573–601.Google Scholar
[2] Dajani, K. and Kraaikamp, C., Ergodic theory of numbers. Carus Mathematical Monographs, 29, Mathematical Association of America, Washington, DC, 2002.Google Scholar
[3] Dafni, G. and Xiao, J., Some new tent spaces and duality theorem for Carleson measures and Qα(Rn). J. Funct. Anal. 208(2004), 377–422. doi:10.1016/S0022-1236(03)00181-2Google Scholar
[4] Dafni, G. and Xiao, J., The dyadic structure and atomic decomposition of Q spaces in several real variables. Tohoku Math. J. 57(2005), no. 1, 119–145. doi:10.2748/tmj/1113234836Google Scholar
[5] Erdös, P., Horváth, M., and Joó, I., On the uniqueness of the expansions 1 = Pq−ni . Acta Math. Hung. 58(1991), no. 3–4, 333–342. doi:10.1007/BF01903963Google Scholar
[6] Erdös, P. and Joó, I., On the expansion 1 = Pq−ni . Period. Math. Hungar. 23(1991), no. 1, 27–30. doi:10.1007/BF02260391Google Scholar
[7] Erdös, P., Joó, I., and Komornik, V., Characterization of the unique expansions 1 = Pq−ni and related problems. Bull. Soc. Math. France 118(1990), no. 3, 377–390.Google Scholar
[8] Essén, M., Janson, S., Peng, L., and Xiao, J., Q spaces of several real variables. Indiana Univ. Math. J. 49(2000), no. 2, 575–615.Google Scholar
[9] Falconer, K., Fractal geometry: Mathematical foundations and applications. John Wiley & Sons, Ltd., Chichester, 1990.Google Scholar
[10] Fefferman, C., Characterization of bounded mean oscillation. Bull. Amer. Math. Soc. 77(1971), 587–588. doi:10.1090/S0002-9904-1971-12763-5Google Scholar
[11] Fefferman, C. and Stein, E. M., Hp spaces of several variables. Acta Math. 129(1972), no. 3–4, 137–193. doi:10.1007/BF02392215Google Scholar
[12] Hueter, I. and Lalley, S. P., Falconer's formula for the Hausdorff dimension of a self-affine set in R2. Ergodic Theory Dynam. Systems 15(1995), no. 1, 77–97. doi:10.1017/S0143385700008257Google Scholar
[13] John, F. and Nirenberg, L., On functions of bounded mean oscillation. Comm. Pure Appl. Math. 14(1961), 415–426. doi:10.1002/cpa.3160140317Google Scholar
[14] Neri, U., Some properties of functions with bounded mean oscillation. Studia Math. 61(1977), no. 1, 63–75.Google Scholar
[15] Stein, E. M., Harmonic analysis: real-variable methods, orthogonality, and oscillatory integrals. Princeton Mathematical Series, 43, Monographs in Harmonic Alalysis, III., Princeton University Press, Princeton, 1993.Google Scholar
[16] Xiao, J., Homothetic variant of fractional Sobolev space with application to Navier-Stokes system. Dyn. Partial Differ. Equ. 4(2007), no. 3, 227–245.Google Scholar
[17] Yue, H. and Dafni, G., A John–Nirenberg inequality for Qα(Rn) spaces. J. Math. Anal. Appl. 351(2009), no. 1, 428–439. doi:10.1016/j.jmaa.2008.10.020Google Scholar