Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-05T14:45:36.892Z Has data issue: false hasContentIssue false
  • English
  • Français

The Fourier Transforms of Smooth Measures on Hypersurfaces of Rn + 1

Published online by Cambridge University Press:  20 November 2018

Bernard Marshall
Bernard Marshall*
Affiliation:
McGill University, Montreal, Quebec
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Fourier transform of the surface measure on the unit sphere in Rn + 1, as is well-known, equals the Bessel function

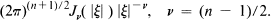
Its behaviour at infinity is described by an asymptotic expansion

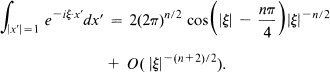
The purpose of this paper is to obtain such an expression for surfaces Σ other than the unit sphere. If the surface Σ is a sufficiently smooth compact n-surface in Rn + 1 with strictly positive Gaussian curvature everywhere then with only minor changes in the main term, such an asymptotic expansion exists. This result was proved by E. Hlawka in [3]. A similar result concerned with the minimal smoothness of Σ was later obtained by C. Herz [2].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 38 , Issue 2 , 01 April 1986 , pp. 328 - 359
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Greenleaf, A., Principal curvature and harmonic analysis, Indiana Math. J. 30 (1981), 519–537.Google Scholar
2. Herz, C., Fourier transforms related to convex sets, Ann. of Math. 75 (1962), 1–36.Google Scholar
3. Hlawka, E., Über Integrale auf konvexen Körpern I, Monatsh. Math. 54 (1950), 1–36; II, ibid. 54 (1950) 81–99.Google Scholar
4. Littman, W., Fourier transforms of surface-carried measures and differentiability of surface averages, Bull. Amer. Math. Soc. 69 (1963), 766–770.Google Scholar
5. Marshall, B., Estimates for solutions of wave equations with vanishing curvature, Can J. Math. 57 (1985).Google Scholar
6. Randol, B., On the Fourier transform of the indicator function of a planar set, Trans. Amer. Math. Soc. 139 (1969), 271–278.Google Scholar
7. Randol, B., On the asymptotic behaviour of the Fourier transform of the indicator function of a convex set, Trans. Amer. Math. Soc. 139 (1969), 279–285.Google Scholar
8. Svensson, I., Estimates for the Fourier transform of the characteristic function of a convex set, Arkiv för Matematik 9 (1971), 11–22.Google Scholar