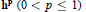Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bloom, Walter R.
and
Xu, Zengfu
2000.
Pseudo differential operators on local Hardy spaces on chébli-teimèche hypergroups.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 68,
Issue. 2,
p.
202.
Jelassi, Mourad
and
Mejjaoli, Hatem
2014.
Fractional Sobolev type spaces associated with a singular differential operator and applications.
Fractional Calculus and Applied Analysis,
Vol. 17,
Issue. 2,
p.
401.
Jelassi, Mourad
and
Mejjaoli, Hatem
2014.
Sobolev-Type Spaces on the Dual of the Chébli-Trimèche Hypergroup and Applications.
Abstract and Applied Analysis,
Vol. 2014,
Issue. ,
p.
1.
Dafni, Galia
Lau, Chun Ho
Picon, Tiago
and
Vasconcelos, Claudio
2022.
Inhomogeneous cancellation conditions and Calderón–Zygmund type operators on hp.
Nonlinear Analysis,
Vol. 225,
Issue. ,
p.
113110.
KUMAR, VISHVESH
and
RUZHANSKY, MICHAEL
2023.
– MULTIPLIERS ON COMMUTATIVE HYPERGROUPS.
Journal of the Australian Mathematical Society,
Vol. 115,
Issue. 3,
p.
375.