Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-20T12:31:36.584Z Has data issue: false hasContentIssue false
  • English
  • Français

Formally Normal Operators Having no Normal Extensions

Published online by Cambridge University Press:  20 November 2018

Earl A. Coddington
Earl A. Coddington*
Affiliation:
University of Copenhagen, University of California, Los Angeles
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

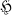The domain and null space of an operator A in a Hilbert space will be denoted by 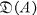and 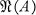, respectively. A formally normal operatorN in 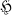is a densely defined closed (linear) operator such that 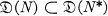, and 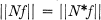for all 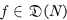A normal operator in 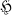is a formally normal operator N satisfying 35 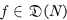. A study of the possibility of extending a formally normal operator N to a normal operator in the given 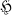, or in a larger Hilbert space, was made in (1).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 17 , 1965 , pp. 1030 - 1040
Copyright
Copyright © Canadian Mathematical Society 1965

References

1. Biriuk, G. and Coddington, E. A., Normal extensions of unbounded formally normal operators, J. Math. Mech., 12 (1964), 617–638.Google Scholar
2. Burchnall, J. L. and Chaundy, T. W., Commutative ordinary differential operators﹜ Proc. London Math. Soc. (Ser. 2), 21 (1923), 420–440.Google Scholar
3. Nelson, E., Analytic vectors, Ann. Math., 70 (1959), 572–615.Google Scholar