Hostname: page-component-6bf8c574d5-xtvcr Total loading time: 0 Render date: 2025-02-21T11:26:12.408Z Has data issue: false hasContentIssue false
  • English
  • Français

A Forcing Axiom Deciding the Generalized Souslin Hypothesis

Part of: Set theory

Published online by Cambridge University Press:  07 January 2019

Chris Lambie-Hanson  and
Assaf Rinot
Chris Lambie-Hanson
Affiliation:
Department of Mathematics, Bar-Ilan University, Ramat-Gan 5290002, Israel Email: [email protected]@math.biu.ac.il
Assaf Rinot
Affiliation:
Department of Mathematics, Bar-Ilan University, Ramat-Gan 5290002, Israel Email: [email protected]@math.biu.ac.il
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We derive a forcing axiom from the conjunction of square and diamond, and present a few applications, primary among them being the existence of super-Souslin trees. It follows that for every uncountable cardinal 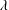$\unicode[STIX]{x1D706}$, if 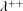$\unicode[STIX]{x1D706}^{++}$ is not a Mahlo cardinal in Gödel’s constructible universe, then 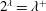$2^{\unicode[STIX]{x1D706}}=\unicode[STIX]{x1D706}^{+}$ entails the existence of a 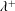$\unicode[STIX]{x1D706}^{+}$-complete 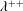$\unicode[STIX]{x1D706}^{++}$-Souslin tree.

Keywords

Souslin treesquarediamondsharply dense setforcing axiomSDFA

MSC classification

Primary: 03E05: Other combinatorial set theory
Secondary: 03E35: Consistency and independence results 03E57: Generic absoluteness and forcing axioms
Type
Article
Information
Canadian Journal of Mathematics , Volume 71 , Issue 2 , April 2019 , pp. 437 - 470
Copyright
© Canadian Mathematical Society 2018 

Footnotes

This research was partially supported by the Israel Science Foundation (grant #1630/14).

References

Brodsky, A. M. and Rinot, A., Distributive Aronszajn trees. To appear in Fundamenta Mathematicae, 2019. http://www.assafrinot.com/paper/29.Google Scholar
Brodsky, A. M. and Rinot, A., A microscopic approach to Souslin-tree constructions. Part I . Ann. Pure Appl. Logic 168(2017), no. 11, 1949–2007. https://doi.org/10.1016/j.apal.2017.05.003.Google Scholar
Brodsky, A. M. and Rinot, A., Reduced powers of Souslin trees . Forum Math. Sigma 5(2017), e2. https://doi.org/10.1017/fms.2016.34.Google Scholar
Devlin, K. J., Aspects of constructibility . Lecture Notes in Mathematics, 354, Springer-Verlag, Berlin-New York, 1973.Google Scholar
Devlin, K. J., Constructibility Perspectives in mathematical logic. Springer-Verlag, Berlin, 1984.Google Scholar
Foreman, M., An ℵ 1-dense ideal on ℵ 2 . Israel J. Math. 108(1998), 253–290. https://doi.org/10.1007/BF02783051.Google Scholar
Foreman, M., Magidor, M., and Shelah, S., Martin’s maximum, saturated ideals and nonregular ultrafilters. II . Ann. of Math. (2) 127(1988), no. 3, 521–545. https://doi.org/10.2307/2007004.Google Scholar
Gitik, M. and Rinot, A., The failure of diamond on a reflecting stationary set . Trans. Amer. Math. Soc. 364(2012), no. 4, 1771–1795. https://doi.org/10.1090/S0002-9947-2011-05355-9.Google Scholar
Jech, T., Non-provability of Souslin’s hypothesis . Comment. Math. Univ. Carolinae 8(1967), 291–305.Google Scholar
Jensen, R. B., The fine structure of the constructible hierarchy . Ann. Math. Logic 4(1972), 229–308. erratum, ibid. 4(1972), 443. https://doi.org/10.1016/0003-4843(72)90001-0.Google Scholar
Jensen, R. B., Souslin’s hypothesis is incompatible with V= L . Notices Amer. Math. Soc 15(1968).Google Scholar
Kurepa, G., Ensembles ordonnés et ramifiés. Publications de l’Institut Mathématique Beograd, 1935.Google Scholar
Lambie-Hanson, C., Aronszajn trees, square principles, and stationary reflection . MLQ Math. Log. Q. 63(2017), no. 3–4, 265–281. https://doi.org/10.1002/malq.201600040.Google Scholar
Laver, R. and Shelah, S., The ℵ 2-Souslin hypothesis . m Trans. Amer. Math. Soc. 264(1981), no. 2, 411–417. https://doi.org/10.2307/1998547.Google Scholar
Mitchell, W., Aronszajn trees and the independence of the transfer property . Ann. Math. Logic 5(1972/73), 21–46. https://doi.org/10.1016/0003-4843(72)90017-4.Google Scholar
Raghavan, D. and Todorcevic, S., Suslin trees, the bounding number, and partition relations. Israel J. Math., to appear.Google Scholar
Rinot, A., Higher Souslin trees and the GCH, revisited . Adv. Math. 311(2017), 510–531. https://doi.org/10.1016/j.aim.2017.03.002.Google Scholar
Shelah, S., Diamonds . Proc. Amer. Math. Soc. 138(2010), no. 6, 2151–2161. https://doi.org/10.1090/S0002-9939-10-10254-8.Google Scholar
Shelah, S., Laflamme, C., and Hart, B., Models with second order properties. V. A general principle . Ann. Pure Appl. Logic 64(1993), no. 2, 169–194. https://doi.org/10.1016/0168-0072(93)90033-A.Google Scholar
Shelah, S. and Stanley, L., S-forcing. I. A “black-box” theorem for morasses, with applications to super-Souslin trees . Israel J. Math. 43(1982), no. 3, 185–224. https://doi.org/10.1007/BF02761942.Google Scholar
Shelah, S. and Stanley, L., S-forcing. IIa. Adding diamonds and more applications: coding sets, Arhangelskii’s problem and ${\mathcal{L}}[Q_{1}^{{<}\unicode[STIX]{x1D714}},Q_{2}^{1}]$ . Israel J. Math. 56(1986), 1–65. https://doi.org/10.1007/BF02776239.Google Scholar
Shelah, S. and Stanley, L., Weakly compact cardinals and nonspecial Aronszajn trees . Proc. Amer. Math. Soc. 104(1988), no. 3, 887–897. https://doi.org/10.2307/2046812.Google Scholar
Solovay, R. M. and Tennenbaum, S., Iterated Cohen extensions and Souslin’s problem . Ann. of Math. (2) 94(1971), 201–245. https://doi.org/10.2307/1970860.Google Scholar
Souslin, M. Y., Problème 3 . Fundamenta Math. 1(1920), no. 1, 223.Google Scholar
Specker, E., Sur un problème de Sikorski . Colloquium Math. 2(1949), 9–12. https://doi.org/10.4064/cm-2-1-9-12.Google Scholar
Tennenbaum, S., Souslin’s problem . Proc. Nat. Acad. Sci. U.S.A. 59(1968), 60–63.Google Scholar
Todorcevic, S., Walks on ordinals and their characteristics . Progress in Mathematics, 263, Birkhäuser Verlag, Basel, 2007.Google Scholar
Todorcevic, S. and Torres Perez, V., Conjectures of Rado and Chang and special Aronszajn trees . MLQ Math. Log. Q. 58(2012), no. 4–5, 342–347. https://doi.org/10.1002/malq.201110037.Google Scholar
Velleman, D., Souslin trees constructed from morasses. In: Axiomatic set theory (Boulder, Colo., 1983), Contemp. Math., 31, American Mathematical Society, Providence, RI, 1984, pp. 219–241. https://doi.org/10.1090/conm/031/763903.Google Scholar
Velleman, D., Morasses, diamond, and forcing . Ann. Math. Logic 23(1982), no. 2–3, 199–281. https://doi.org/10.1016/0003-4843(82)90005-5.Google Scholar
Zwicker, W. S., $P_{k}\unicode[STIX]{x1D706}$  combinatorics. I. Stationary coding sets rationalize the club filter. In: Axiomatic set theory (Boulder, Colo., 1983), Contemp. Math., 31, American Mathematic Society, Providence, RI, 1984, pp. 243–259. https://doi.org/10.1090/conm/031/763904.Google Scholar