Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-19T11:22:52.786Z Has data issue: false hasContentIssue false
  • English
  • Français

Fluctuations Pour Des Équations De Boltzmann Scalaires

Published online by Cambridge University Press:  20 November 2018

René Ferland
René Ferland*
Affiliation:
Université du Québec à Montréal, Montréal, Québec
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Kac [22] a montré, pour sa caricature d'un gaz de Boltzmann, que la solution de l'équation de Boltzmann généralisée correspondante peut être obtenue comme limite d'une suite de lois empiriques induites par des processus markoviens 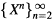. Pour un entier n donné, le processus (Xn(t))t≥0 décrit le comportement d'un gaz à n molécules où des collisions binaires ont lieu à des instants imprévisibles. Ce processus est gouverné par un générateur Gn qui est défini à l'aide de l'opérateur de collision apparaissant dans la version de Kac de l'équation de Boltzmann.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 43 , Issue 5 , 01 October 1991 , pp. 975 - 984
Copyright
Copyright © Canadian Mathematical Society 1991

References

1. Barnsley, M.F. and Turchetti, G., A Study ofBoltzmann energy equations, Ann. Phys. 159 (1985), 1–61.Google Scholar
2. Billingsley, P., Convergence of probability measures. Wiley, New York, 1968.Google Scholar
3. Bobylev, A.V., Exact solutions of the Boltzmann equation, Soviet Phys. Dokl. 20 (1976), 822–824.Google Scholar
4. Bobylev, A.V., A class of invariant solutions of the Boltzmann equation, Soviet Phys. Dokl. 21 (1976), 632–634.Google Scholar
5. Braun, W. and Hepp, K., The Vlasov dynamics and its fluctuations in the 1/N limit of interacting classical particles, Commun. Math. Phys. 56 (1977), 101–113.Google Scholar
6. Chapman, S. and Cowling, T.G., The Mathematical theory of non-uniform gases. Cambridge University Press, London, 1970.Google Scholar
7. Duderstadt, J.J. and Martin, W.R., Transport theory. Wiley, New York, 1979.Google Scholar
8. Ernst, M.H., Nonlinear model-Boltzmann equations and exact solutions, Phys. Rep. 78 (1981), 1–171.Google Scholar
9. Ernst, M.H. and Hendriks, E.M., An exactly solvable non-linear Boltzmann equation, Phys. Lett. A 70 (1979), 183–185.Google Scholar
10. Ethier, S.N. and Kurtz, T.G., Markov processes. Characterization and convergence. Wiley, New York, 1986.Google Scholar
11. Ferland, R. and Giroux, G., Cutoff-type Boltzmann equations: Convergence of the solution, Adv. in Appl. Math. 8 (1987), 98–107.Google Scholar
12. Ferland, R., Équations de Boltzmann scalaires : convergence de la solution, fluctuationset propagation du chaos trajectorielle. Thèse de doctorat, Université de Sherbrooke, 1990.Google Scholar
13. Fernique, X., Fonctions aléatoires à valeurs dans les espaces lusiniens, preprint.Google Scholar
14. Fernique, X., Vecteurs aléatoires lusiniens et fonctions aléatoires lusiniennes. Rapport de recherche no 67, Département de mathématiques et d'informatique, Université de Sherbrooke, 1989.Google Scholar
15. Futcher, F.J., Hoare, M.R., Hendriks, E.M. and Ernst, M.H., Soluble Boltzmann equations for internal state and Maxwell models, Phys. A 101 (1980), 185–204.Google Scholar
16. Futcher, F.J. and Hoare, M.R., The p-q model Boltzmann equation, Phys. A 122 (1983), 516–546.Google Scholar
17. Gartner, J., On the McKean-Vlasov limit for interacting diffusions, Math. Nachr. 137 (1988), 197–248.Google Scholar
18. Holley, R.A. and Stroock, D.V., Generalized Ornstein-Uhlenbeckprocesses and infinite particle branching Brownian motion, Publ. Res. Inst. Math. Sci. 14 (1978), 741–788.Google Scholar
19. Hoare, M.H., Quadratic transport and soluble Boltzmann equation, Adv. Chem. Phys. 56 (1984), 1–140.Google Scholar
20. Huxley, L.G.H. and Crompton, R.W., The Diffusion and drift of electrons in gases. Wiley, New York, 1974.Google Scholar
21. Jakubowski, A., On the Skorokhod topology, Ann. Inst. Henri Poincaré 22 (1986), 263–285.Google Scholar
22. Kac, M., Foundations of kinetic theory, Proc. Third Berkeley Symp. Math. Statist. Prob. (J. Neyman, ed.) 3 (1956), 171–197.Google Scholar
23. Kac, M., Some probabilistic aspects of the Boltzmann-equation, Acta Phys. Austriaca Suppl. 10 (1973), 379–400.Google Scholar
24. Kesten, H., Quadratic transformations: a model for population growth I, Adv. in Appl. Probab. 2 (1970), 1–82.Google Scholar
25. Kesten, H., Quadratic transformations: a model for population growth II, Adv. in Appl. Probab. 2 (1970), 179–228.Google Scholar
26. Krook, M. and Wu, T.T., Formation ofMaxwellian tails, Phys. Rev. Lett. 36 (1976), 1107–1109.Google Scholar
27. Krook, M. and Wu, T.T., Exact solutions of the Boltzmann equation, Phys. Fluids 20 (1977), 1589–159.Google Scholar
28. McKean, H.P., Fluctuations in the kinetic theory of gases, Comm. Pure Appl. Math. 28 (1975), 435–455.Google Scholar
29. Moran, P.A.P., The Statistical processes of evolutionary theory. Clarendon Press, Oxford, 1962.Google Scholar
30. Nishimura, S., Random collision processes and their limiting distribution using the discrimination information, J. Appl. Probab. 11 (1974), 266–280.Google Scholar
31. Nishimura, S., Random collision processes with transition probabilities belonging to the same type of distribution, J. Appl. Probab. 11 (1974), 703–714.Google Scholar
32. Rankin, C.C. and Light, J.C., Relaxation of a gas of harmonic oscillators, J. Chem. Phys. 46 (1967), 1305-1316.Google Scholar
33. Shuler, K.E., Relaxation of an isolated ensemble of harmonic oscillators, J. Chem. Phys. 32 (1960), 1692- 1697.Google Scholar
34. Tanaka, H., Propagation of chaos for certain purely discontinuous Markov processes with interaction, J. Fac. Sci. Univ. Tokyo Sect. IA Math. 17 (1970), 253–272.Google Scholar
35. Tanaka, H., Fluctuation theory for Kacs one-dimensional model ofMaxwellian molecules, Sankhyā Ser. A 44 (1982), 23–26.Google Scholar
36. Tanaka, H., Some probabilistic problems in the spatially homogeneous Boltzmann equation. Proc. of IFIP-ISI Conf. Theo. Appl. of Random Fields, Bangalore, 1982.Google Scholar
37. Tjon, J. and Wu, T.T., Numerical aspects of the approach to a Maxwellian distribution. Phys. Rev. A 19 (1979), 883–888.Google Scholar
38. Uchiyama, K., Fluctuations ofMarkovian systems in Kacs caricature of a Maxwellian gas, J. Math. Soc. Japan 35 (1983), 477–199.Google Scholar
39. Uchiyama, K., A fluctuation problem associated with the Boltzmann equation for a gas of molecules with a cutoff potential, Japan. J. Math. 9 (1983), 27–53.Google Scholar
40. Uchiyama, K., Fluctuations in population dynamics. Lecture Notes in Biomath. 70, Springer-Verlag, New York, 1986, 222–229.Google Scholar
41. Wu, T.T., Kinetic equations of gases and plasmas. Addison-Wesley, Reading, 1966.Google Scholar