Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T00:49:57.401Z Has data issue: false hasContentIssue false
  • English
  • Français

Extremal Properties of Constrained Tchebychev Polynomials

Published online by Cambridge University Press:  20 November 2018

R. Pierre
R. Pierre*
Affiliation:
Université Laval, Québec, Québec
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In the sequel, πn will denote the class of real polynomials of degree at most n and ‖f(x)‖∞ the L∞-norm of a function on [–l, +1].

In a series of recent papers, Saff and Varga studied the properties of the so-called incomplete polynomials; that is to say polynomials of the form

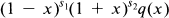
where sl and s2 are fixed integers and q ∊ πn.

In there, they define the constrained Tchebychev polynomial as being, up to a multiplicative constant, the solution of the following minimization problem

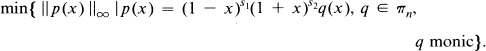
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 38 , Issue 4 , 01 August 1986 , pp. 907 - 924
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Duffin, R. J. and Schaeffer, A. C., On some inequalities of S. Bernstein and W. Markov for derivatives of polynomials, Bull. Am. Math. Soc. 44 (1938), 289–297.Google Scholar
2. Lachance, M. A., Bernstein and Markov inequalities for constrained polynomials, manuscript, to appear.Google Scholar
3. Lachance, M., Saff, E. B. and Varga, R. S., Bounds for incomplete polynomials vanishing at both end points of an interval, in Constructive approaches to mathematical models (Academic Press, New York, 1979), 421–437.Google Scholar
4. Pierre, R. and Rahman, Q. I., On polynomials with curved majorants, Studies in Pure Mathematics 4 (1981), KOCZOGH, 5.6.Google Scholar
5. Pierre, R. and Rahman, Q. I., On a problem of Turan about polynomials, Proc. Amer. Math. Soc. 56 (1976), 231–238.Google Scholar
6. Pierre, R. and Rahman, Q. I., On a problem of Turan III, Can. J. Math. 34 (1982), 888–899.Google Scholar
7. Schur, I., Über das maximum des absoluten bestrages eines polynoms in einem gegebenen interval, Math. Zeit. 4 (1919), 271–287.Google Scholar