No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
A set of points (edges) of a graph is independent if no two distinct members of the set are adjacent. Gallai (1) observed that, if A0 (B0) is the minimum number of points (edges) of a finite graph covering all the edges (points) and A1 (B1) is the maximum number of independent points (edges), then:
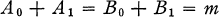
holds, where m is the number of points of the graph.
The concepts of independence and covering are generalized in various ways for n-graphs. In this paper we establish certain connections between the corresponding extreme numbers analogous to the above result of Gallai.
Ray-Chaudhuri considered (2) independence and covering problems in n-graphs and determined algorithms for finding the minimal cover and some associated numbers.