Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-20T16:22:06.443Z Has data issue: false hasContentIssue false
  • English
  • Français

Extensions of Pseudometrics

Published online by Cambridge University Press:  20 November 2018

H. L. Shapiro
H. L. Shapiro*
Affiliation:
The Pennsylvania State University, University Park, Pennsylvania
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

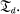If γ is an infinite cardinal number, a subset S of a topological space X is said to be Pγ-embedded in X if every γ-separable continuous pseudometric on S can be extended to a γ-separable continuous pseudometric on X. (A pseudometric d on X is γ-separable if there exists a subset G of X such that |G| ⩽ 7 and such that G is dense in X relative to the pseudometric topology A pseudometric d is continuous if d is continuous relative to the product topology on X × X.) We say that S is P-embedded in X if every continuous pseudometric on S can be extended to a continuous pseudometric on X.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 18 , 1966 , pp. 981 - 998
Copyright
Copyright © Canadian Mathematical Society 1966

References

1. Arens, Richard, Extension of junctions on fully normal spaces, Pacific J. Math., 2 (1952), 11–22.Google Scholar
2. Arens, Richard, Extension of coverings, of pseudometrics, and of linear-space-valued mappings, Can. J. Math., 5 (1953), 211–215.Google Scholar
3. Bing, R. H., Extending a metric, Duke Math. J., 14 (1947), 511–519.Google Scholar
4. Bing, R. H., Metrization of topological spaces, Can. J. Math., 3 (1951), 175–186.Google Scholar
5. Bourbaki, N., Topologie générale, 2nd ed. (Paris, 1948), Chap. IX.Google Scholar
6. Corson, H. H., Normality in subsets of product spaces, Amer. J. Math., 81 (1959), 785–796.Google Scholar
7. Dieudonné, Jean, Une généralisation des espaces compacts, J. Math. Pures Appl., 23 (1944), 65–76.Google Scholar
8. Dowker, C. H., On countably paracompact spaces, Can. J. Math., 3 (1951), 219–224.Google Scholar
9. Dowker, C. H., On a theorem of Banner, Ark. Mat., 2 (1952), 307–313.Google Scholar
10. Frink, A. H., Distance-functions and the metrization problem, Bull. Amer. Math. Soc., 43 (1937), 133–142.Google Scholar
11. Gillman, L. and Jerison, M., Rings of continuous functions (New York, 1960).Google Scholar
12. Ginsburg, Seymour and Isbell, J. R., Some operators on uniform spaces, Trans. Amer. Math. Soc., 93 (1959), 143–168.Google Scholar
13. Hausdorff, F., Erweiterung einer Homöomorphie’, Fund. Math., 16 (1930), 353–360.Google Scholar
14. Iséki, Kiyoshi and Kasahara, Shouro, On pseudo-compact and countably compact spaces, Proc. Japan Acad., 33 (1957), 100–102.Google Scholar
15. Katětov, Miroslav, Extension of locally finite covers, Colloq. Math., 6 (1958), 145–151 (Russian).Google Scholar
16. Kelley, J. L., General topology (New York, 1955).Google Scholar
17. Lefschetz, S., Algebraic topology (New York, 1942).Google Scholar
18. Mack, John, On a class of countably paracompact spaces, Proc. Amer. Math. Soc., 16 (1965), 467–472.Google Scholar
19. Michael, E., Review of On a theorem of Hanner by Dowker, C. H., Math. Rev., 14 (1953), 396.Google Scholar
20. Michael, E., Point-finite and locally finite coverings, Can. J. Math., 7 (1955), 275–279.Google Scholar
21. Morita, Kiiti, Star-finite coverings and the star-finite property, Math. Japon., 1 (1948), 60–68.Google Scholar
22. Morita, Kiiti, On the dimension of normal spaces., II, J. Math. Soc. Japan, 2 (1950), 16–33.Google Scholar
23. Paracompactness and product spaces, Fund. Math., 50 (1962), 223–236.Google Scholar
24. Stone, A. H., Review of Extension of coverings, of pseudometrics, and of linear-s pace-valued mappings by Arens, Richard, Math. Rev., 14 (1953), 1108.Google Scholar
25. Tukey, J. W., Convergence and uniformity in topology (Princeton, 1940).Google Scholar