In this paper we consider Banach space automorphisms of m, the space of bounded sequences, which map c, the space of convergent sequences, into itself. In particular, we consider the problem of determining which maps from C0, the space of sequences converging to 0, to c can be extended to such automorphisms.

The origin of this note lies in an incorrect conjecture of mine. If the automorphism T: m → m is given by a matrix, that is, a sequence of elements of ll, and if T is conservative, that is, T(c) ⊂ c, then T(c) = c. That is, T restricted to c is an automorphism of c. We had hoped this would hold even if T were not a matrix. We can see, for example, that if the conservative automorphism T is bounded on the unit cube of m by 1 and ρ, where 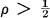, then T(c) = c. However, in general it is possible for a conservative automorphism of m to map c properly into c.