Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T01:14:07.944Z Has data issue: false hasContentIssue false
  • English
  • Français

The Extensions of an Invariant Mean and the Set LIM ∽ TLIM

Published online by Cambridge University Press:  20 November 2018

Tianxuan Miao
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

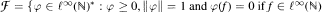Let with 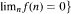. If G is a nondiscrete locally compact group which is amenable as a discrete group and m ∈ LIM(CB(G)), then we can embed 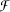into the set of all extensions of m to left invariant means on L∞(G) which are mutually singular to every element of TLIM(L∞(G)), where LIM(S) and TLIM(S) are the sets of left invariant means and topologically left invariant means on S with S = CB(G) or L∞(G). It follows that the cardinalities of LIM(L∞(G)) ̴ TLIM(L∞(G)) and LIM(L∞(G)) are equal. Note that 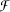which contains 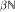is a very big set. We also embed 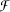into the set of all left invariant means on CB(G) which are mutually singular to every element of TLIM(CB(G)) for G = G1 ⨯ G2, where G1 is nondiscrete, non–compact, σ–compact and amenable as a discrete group and G2 is any amenable locally compact group. The extension of any left invariant mean on UCB(G) to CB(G) is discussed. We also provide an answer to a problem raised by Rosenblatt.

Keywords

43A07locally compact groupsamenable groupsinvariant meansthe set of left invariant means
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 46 , Issue 4 , 01 August 1994 , pp. 808 - 817
Copyright
Copyright © Canadian Mathematical Society 1994

References

1. Chou, C., On topological invariant means on a locally compact group, Trans. Amer. Math. Soc. 151(1970), 443–456.Google Scholar
2. Chou, C., Topological invariant means on the von Neumann algebra VN(G), Trans. Amer. Math. Soc. 273(1982), 209–229.Google Scholar
3. Granirer, E. E., Criteria for compactness and for discreteness of locally compact amenable groups, Proc. Amer. Math. Soc. 40(1973), 615–624.Google Scholar
4. Greenleaf, F. P., Invariant Means on Topological Groups, Van Nostrand, New York, 1969.Google Scholar
5. Lau, A. T. and Paterson, A. L. T., The exact cardinality of the set of topological left invariant means on an amenable locally compact group, Proc. Amer. Math. Soc. 98(1986), 75–80.Google Scholar
6. Liu, T. S. and van Rooij, A., Invariant means on a locally compact group, Monatsh. Math. 78(1974), 356–359.Google Scholar
7. Miao, T., Amenability of locally compact groups and subspaces of L∞(G), Proc. Amer. Math. Soc. 111 (1991), 1075–1084.Google Scholar
8. Miao, T., On the sizes of the sets of invariant means, Illinois J. Math. 36(1992), 53–72.Google Scholar
9. Paterson, A. L. T., Amenability, Amer. Math. Soc, Providence, Rhode Island, 1988.Google Scholar
10. Pier, J. P., Amenable Locally Compact Groups, Wiley, New York, 1984.Google Scholar
11. Reiter, H., Classical harmonic analysis and locally compact groups, Oxford Math. Monographs (1968),.Google Scholar
12. Rosenblatt, J. M., Invariant means and invariant ideals in L∞(G)fora locally compact group G, J. Funct. Anal. 21(1976), 31–51.Google Scholar
13. Rosenblatt, J. M., Invariant means for the bounded measurable functions on a non-discrete locally compact group, Math. Ann. 220(1976), 219–228.Google Scholar
14. Rosenblatt, J. M., Invariant menas on the continuous bounded functions, Trans. Amer. Math. Soc. 236(1978), 315–324.Google Scholar
15. Rosenblatt, J. M., The number of extensions of an invariant mean, Compositio Math. 33(1976), 147–159.Google Scholar
16. Rudin, W., Invariant mean on L∞ , Studia Math. 44(1972), 219–227.Google Scholar
17. Talagrand, M., Géométrie des simplexes de moyennes invariantes, J. Funct. Anal. 34(1979), 304–337.Google Scholar
18. Yosida, K., Functional Analysis, Fourth Edition, Springer-Verlag, Berlin, Heidelberg, New York, 1974.Google Scholar