Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T01:16:33.749Z Has data issue: false hasContentIssue false
  • English
  • Français

Extensions by Simple C*-Algebras: Quasidiagonal Extensions

Published online by Cambridge University Press:  20 November 2018

Huaxin Lin
Huaxin Lin*
Affiliation:
Department of Mathematics, University of Oregon, Eugene, Oregon 97403-1222, U.S.A. and Department of Mathematics, East China Normal University, Shanghai, China
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

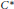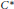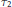Let $A$ be an amenable separable ${{C}^{*}}$-algebra and $B$ be a non-unital but $\sigma $-unital simple ${{C}^{*}}$- algebra with continuous scale. We show that two essential extensions ${{\tau }_{1}}$ and ${{\tau }_{2}}$ of $A$ by $B$ are approximately unitarily equivalent if and only if

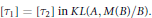$$\left[ {{\tau }_{1}} \right]\,=\,\left[ {{\tau }_{2}} \right]\,\text{in}\,KL\left( A,\,M\left( B \right)/B \right).$$

If $A$ is assumed to satisfy the Universal Coefficient Theorem, there is a bijection from approximate unitary equivalence classes of the above mentioned extensions to 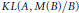$KL\left( A,\,M\left( B \right)/B \right)$. Using 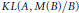$KL\left( A,\,M\left( B \right)/B \right)$, we compute exactly when an essential extension is quasidiagonal. We show that quasidiagonal extensions may not be approximately trivial. We also study the approximately trivial extensions.

Keywords

46L0546L35
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 57 , Issue 2 , 01 April 2005 , pp. 351 - 399
Copyright
Copyright © Canadian Mathematical Society 2005

References

[AP] Akemann, C. A. and Pedersen, G. K., Central sequences and inner derivations of separable C*-algebras. Amer. J. Math. 101(1979), 1047–1061.Google Scholar
[AS] Akemann, C. A. and Shultz, F. W., Perfect C*-algebras. Mem. Amer.Math. Soc. no. 326, 1985.Google Scholar
[BH] Blackadar, B. and Handelman, D., Dimension functions and traces on C*-algebras. J. Funct. Anal. 45(1982), 297-340.Google Scholar
[BK] Blackadar, B. and Kirchberg, E., Generalized inductive limits of finite-dimensional C*-algebras. Math. Ann. 307(1997), 343–380.Google Scholar
[Br1] Brown, L. G., Stable isomorphism of hereditary subalgebras of C*-algebras. Pacific J. Math. 71(1977), 335–348.Google Scholar
[Br2] Brown, L. G., The universal coefficient theorem for Ext and quasidiagonality. Operator Algebras and Group Representations, 17, Pitman Press, Boston, 1983, pp. 60–64.Google Scholar
[BDF1] Brown, L. G., Douglas, R. G. and Fillmore, P. A., Unitary equivalence modulo the compact operators and extensions of C*-algebras. Proceedings of a Conference on Operator Theory, Lecture Notes in Math. 345, Springer, Berlin, 1973, pp. 58–128.Google Scholar
[BDF2] Brown, L. G., Douglas, R. G. and Fillmore, P. A., Extensions of C*-algebras, operators with compact self-commutators and K-homology. Bull. Amer. Math. Soc. 79(1973), 973–978.Google Scholar
[BDF3] Brown, L. G., Douglas, R. G. and Fillmore, P. A., Extensions of C*-algebras and K-homology. Ann. of Math. 105(1977), 265–324.Google Scholar
[CE] Choi, M. D. and Effros, E., The completely positive lifting problem for C*-algebras, Ann. of Math. 104(1976), 585–609.Google Scholar
[DL] Dadarlat, M. and Loring, T., A universal multi-coefficient theorem for the Kasparov groups. Duke J. Math. 84(1996), 355–377.Google Scholar
[EHS] Effros, E., Handelman, D. and Shen, C.-L., Dimension groups and their affine representations. Amer. J. Math. 102(1980), 385–407.Google Scholar
[Ell1] Elliott, G. A., On the classification of C*-algebras of real rank zero. J. Reine Angew.Math. 443(1993), 179–219.Google Scholar
[EG] Elliott, G. A. and Gong, G., On the classification of C*-algebras of real rank zero, II. Ann. of Math. 144(1996), 497–610.Google Scholar
[Fu] Fuchs, L., Infinite Abelian Groups. Academic Press, New York, 1973.Google Scholar
[GL] Gong, G. and Lin, H., Almost multiplicative morphisms and K-theory. Internat. J. Math. 11(2000), 983–1000.Google Scholar
[K1] Kirchberg, E., Classification of purely infinite simple C*-algebras by Kasparov groups. third draft, 1996.Google Scholar
[KP] Kirchberg, E. and Phillips, N. C., Embedding of exact C*-algebras in the Cuntz algebra O2, J. Reine Angew.Math. 525(2000), 17–53.Google Scholar
[H] Halmos, P. R., The problems in Hilbert space. Bull. Amer. Math. Soc. 76(1970), 887–933.Google Scholar
[Ln1] Lin, H., Simple C*-algebras with continuous scales and simple corona algebras. Proc. Amer. Math. Soc. 112(1991), 871–880 Google Scholar
[Ln2] Lin, H., Notes on K-theory of multiplier algebras, preprint 1991.Google Scholar
[Ln3] Lin, H., Exponential rank of C*-algebras with real rank zero and the Brown-Pedersen conjectures. Funct, J.. Anal. 114(1993), 1–11.Google Scholar
[Ln4] Lin, H., Generalized Weyl-von Neumann theorem. II. Math. Scand. 77(1995), 128–147.Google Scholar
[Ln5] Lin, H., C*-algebra Extensions of C(X). Memoirs Amer.Math. Soc. 550, 115(1995).Google Scholar
[Ln6] Lin, H., Extensions by C*-algebras with real rank zero. II. Proc. LondonMath. Soc. 71(1995), 641–674.Google Scholar
[Ln7] Lin, H., Extensions by C*-algebras with real rank zero. III. Proc. LondonMath. Soc. 76(1998), 634–666.Google Scholar
[Ln8] Lin, H., Extensions of C(X) by simple C*-algebras of real rank zero. Amer. J. Math. 119(1997), 1263–1289.Google Scholar
[Ln10] Lin, H., Stable approximate unitary equivalence of homomorphisms. J. Operator Theory 47(2002), 343–378.Google Scholar
[Ln16] Lin, H., An Introduction to the Classification of Amenable C*-Algebras,World Scientific, River Edge, NJ, 2001.Google Scholar
[Ln17] Lin, H., Classification of simple C*-algebras with tracial topological rank zero. MSRI preprint 2000.Google Scholar
[Ln18] Lin, H., An Approximate Universal Coefficient Theorem, preprint 2001.Google Scholar
[Ln19] Lin, H., A separable version of Brown-Douglas-Fillmore Theorem and weak stability, preprint, 2002.Google Scholar
[Ln20] Lin, H., Semiprojectivity for purely infinite simple C*-algebras, preprint 2002.Google Scholar
[Ln21] Lin, H., Simple corona algebras, preprint.Google Scholar
[Ph1] Phillips, N. C., A classification theorem for nuclear purely infinite simple C*-algebras. Doc. Math. 5(2000), 49–114.Google Scholar
[Ro1] Rørdam, M., Classification of inductive limits of Cuntz algebras. J. Reine Angew.Math. 440(1993), 175–200.Google Scholar
[Ro2] Rørdam, M., A short proof of Elliott's theorem: O2 ⊗ O2 ≌ O2, Math, C. R.. Rep. Acad. Sci. Canada 16(1994), 31–36.Google Scholar
[Ro3] Rørdam, M., Classification of certain infinite simple C*-algebras. III. In: Operator algebras and their applications, Fields Inst. Commun., 13, Amer. Math. Soc., Providence, RI, 1997, pp. 257–282.Google Scholar
[Ro4] Rørdam, M., Classification of nuclear, simple C*-algebras. Classification of nuclear C*-algebras, Entropy in operator algebras. Encyclopaedia Math. Sci. 126, Springer, Berlin, 2002, pp. 1–145.Google Scholar
[Ro5] Rørdam, M., Simple C*-algebras with finite and infinite projections, preprint.Google Scholar
[Rot] Rotman, J., Torsion free and mixed abelian groups. Illinois J. Math, 5(1961), 131–143.Google Scholar
[Sa] Salinas, N., Relative quasidiagonality and KK-theory. Houston J. Math. 18(1992), 97–116.Google Scholar
[Sc1] Schochet, C., Topological methods for C*-algebras IV: mod p homology. Pacific J. Math. 114(1984), 447–468.Google Scholar
[Sc2] Schochet, C., The fine structure of the Kasparov groups II: Relative quasidiagonality, preprintGoogle Scholar
[V1] Voiculescu, D., A note on quasi-diagonal C*-algebras and homotopy. Duke Math. J. 62(1991), 267–271.Google Scholar
[V2] Voiculescu, D., Around quasidiagonal operators. Integral Equat. Operator Theory 17(1993), 137–148.Google Scholar
[Zh1] Zhang, S., On the structure of projections and ideals of corona algebras. Canad. J. Math. 41(1989), 721–742.Google Scholar
[Zh2] Zhang, S., Diagonalizing projections in multiplier algebras and in matrix over a C*-algebra. Pacific J. Math. 145(1990), 181–200.Google Scholar
[Zh3] Zhang, S., A property of purely infinite simple C*-algebras, Proc. Amer.Math. Soc. 109(1990), 717–720.Google Scholar