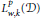Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Björn, Jana
and
Shanmugalingam, Nageswari
2007.
Poincaré inequalities, uniform domains and extension properties for Newton–Sobolev functions in metric spaces.
Journal of Mathematical Analysis and Applications,
Vol. 332,
Issue. 1,
p.
190.
Chua, Seng-Kee
2009.
Sobolev interpolation inequalities on generalized John domains.
Pacific Journal of Mathematics,
Vol. 242,
Issue. 2,
p.
215.
Chua, Seng-kee
and
Wheeden, Richard
2011.
Self-improving properties of inequalities of Poincaré type ons-John domains.
Pacific Journal of Mathematics,
Vol. 250,
Issue. 1,
p.
67.
Brewster, Kevin
Mitrea, Dorina
Mitrea, Irina
and
Mitrea, Marius
2014.
Extending Sobolev functions with partially vanishing traces from locally(ε,δ)-domains and applications to mixed boundary problems.
Journal of Functional Analysis,
Vol. 266,
Issue. 7,
p.
4314.
Chua, Seng-Kee
and
Wheeden, Richard L.
2017.
Existence of weak solutions to degenerate p-Laplacian equations and integral formulas.
Journal of Differential Equations,
Vol. 263,
Issue. 12,
p.
8186.
Castro, Hernán
and
Cornejo, Marco
2023.
Poincaré's inequality and Sobolev spaces with monomial weights.
Mathematische Nachrichten,
Vol. 296,
Issue. 10,
p.
4500.
Cejas, María Eugenia
Mosquera, Carolina
Pérez, Carlos
and
Rela, Ezequiel
2023.
Self-improving Poincaré-Sobolev type functionals in product spaces.
Journal d'Analyse Mathématique,
Vol. 149,
Issue. 1,
p.
1.
Siclari, Giovanni
2024.
On the fractional powers of a Schrödinger operator with a Hardy-type potential.
Proceedings of the Edinburgh Mathematical Society,
Vol. 67,
Issue. 2,
p.
460.
Bechtel, Sebastian
Brown, Russell M.
Haller, Robert
and
Tolksdorf, Patrick
2025.
Extendability of functions with partially vanishing trace.
Annales de l'Institut Fourier,
p.
1.
Kijaczko, Michał
2025.
Asymptotics of weighted Gagliardo seminorms.
Annali di Matematica Pura ed Applicata (1923 -),