Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T00:44:56.382Z Has data issue: false hasContentIssue false
  • English
  • Français

Extending Algebras to Model Congruence Schemes

Published online by Cambridge University Press:  20 November 2018

J. Berman ,
G. Grätzer  and
C. R. Platt
J. Berman
Affiliation:
University of Illinois at Chicago, Chicago, Illinois
G. Grätzer
Affiliation:
University of Manitoba, Winnipeg, Manitoba
C. R. Platt
Affiliation:
University of Manitoba, Winnipeg, Manitoba
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper is concerned with the description of principal congruence relations. Given elements a and b of a universal algebra 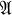, let θ(a, b) denote the smallest congruence relation on 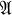containing the pair 〈a, b〉. One of the earliest characterizations of θ(a, b) is Mal'cev's well-known result [5, Theorem 1.10.3], which says that c ≡ d(θ(a, b)) if and only if there exists a sequence z0, z1, …, zn of elements of 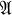and a sequence f1, f2, …, fn of unary algebraic functions such that c = z0, d = zn, and for each i = 1, …, n,

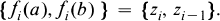
Although this describes θ(a, b) in terms of a set of unary algebraic functions, it is not possible to predict the number or complexity of the unary functions used independently of the choice of a, b, c and d. Several recent papers ([1], [2], [3], [4], [6]) investigate classes of algebras in which principal congruences are simpler.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 38 , Issue 2 , 01 April 1986 , pp. 257 - 276
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Baldwin, J. T. and Berman, J., Definable principal congruence relations: kith and kin, Acta. Math. Sci. Szeged 44 (1982), 255–270.Google Scholar
2. Berman, J. and Grätzer, G., Uniform representations of congruence schemes, Pacific J. Math 76 (1978), 301–311.Google Scholar
3. Blok, W. J. and Pigozzi, D., On the structure of varieties with equationally definable principal congruences. I, Algebra Universalis 15 (1982), 195–227.Google Scholar
4. Fried, E., Grätzer, G., and Quackenbush, R. W., Uniform congruence schemes, Algebra Universalis 70 (1980), 176–188.Google Scholar
5. Grätzer, G., Universal algebra, Second Edition (Springer Verlag, New York, Heidelberg, Berlin, 1979).Google Scholar
6. Köhler, P. and Pigozzi, D., Varieties with equationally defined principal congruences, Algebra Universalis 11 (1980), 213–219.Google Scholar