Let G be a finite graph with non-empty vertex set 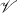(G) and edge set 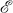(G) (see [2]). Let λ be a positive integer. Tutte [5] defines a λ-colouring of G as a mapping of 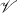(G) into the set Iλ = {1, 2, 3, …, λ} with the property that two ends of any edge are mapped onto distinct integers. The elements of Iλ are commonly called “colours.” If P(G, λ) represents the number of λ-colourings of G, it is well known that P(G, λ) can be expressed as a polynomial in λ. For this reason P(G, λ) is usually referred to as the chromatic polynomial of G.

The chromatic polynomial P(G, λ) was first suggested as an approach to the four-colour conjecture. To quote Tutte [5]: ”… many people are specially interested in the value λ = 4.