No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
Let 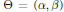 $\Theta \,=\,\left( \alpha ,\,\beta \right)$ be a point in
$\Theta \,=\,\left( \alpha ,\,\beta \right)$ be a point in 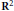 ${{\text{R}}^{2}}$, with
${{\text{R}}^{2}}$, with 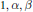 $1,\,\alpha ,\,\beta $ linearly independent over
$1,\,\alpha ,\,\beta $ linearly independent over 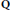 $\mathrm{Q}$. We attach to
$\mathrm{Q}$. We attach to 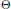 $\Theta $ a quadruple
$\Theta $ a quadruple 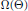 $\Omega \left( \Theta \right)$ of exponents that measure the quality of approximation to
$\Omega \left( \Theta \right)$ of exponents that measure the quality of approximation to 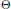 $\Theta $ both by rational points and by rational lines. The two “uniform” components of
$\Theta $ both by rational points and by rational lines. The two “uniform” components of 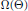 $\Omega \left( \Theta \right)$ are related by an equation due to Jarník, and the four exponents satisfy two inequalities that refine Khintchine's transference principle. Conversely, we show that for any quadruple
$\Omega \left( \Theta \right)$ are related by an equation due to Jarník, and the four exponents satisfy two inequalities that refine Khintchine's transference principle. Conversely, we show that for any quadruple 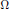 $\Omega $ fulfilling these necessary conditions, there exists a point
$\Omega $ fulfilling these necessary conditions, there exists a point 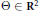 $\Theta \,\in \,{{\text{R}}^{2}}$ for which
$\Theta \,\in \,{{\text{R}}^{2}}$ for which 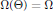 $\Omega \left( \Theta \right)\,=\,\Omega $.
$\Omega \left( \Theta \right)\,=\,\Omega $.