Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T01:14:06.658Z Has data issue: false hasContentIssue false
  • English
  • Français

Exponential Boundedness and Amenability of Open Subsemigroupsof Locally Compact Groups

Published online by Cambridge University Press:  20 November 2018

Wojciech Jaworski
Wojciech Jaworski*
Affiliation:
Department of Mathematics, University of Ottawa, Ottawa, OntarioK1N6N5
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a connected amenable locally compact group with left Haar measure λ. In an earlier work Jenkins claimed that exponential boundedness of G is equivalent to each of the following conditions: (a) every open subsemigroup S ⊆ G is amenable; (b) given 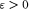and a compact K ⊆ G with nonempty interior there exists an integer n such that (c) given a signed measure of compact support and nonnegative nonzero f ∈ L∞(G), the condition v * f ≥ 0 implies v(G) ≥ 0. However, Jenkins‚ proof of this equivalence is not complete. We give a complete proof. The crucial part of the argument relies on the following two results: (1) an open σ-compact subsemigroup S ⊆ G is amenable if and only if there exists an absolutely continuous probability measure μ on S such that lim 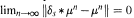for every s ∈ S; (2) G is exponentially bounded if and only if 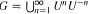for every nonempty open subset U ⊆ G.

Keywords

43A0722D0543A0560B15
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 46 , Issue 6 , 01 December 1994 , pp. 1263 - 1274
Copyright
Copyright © Canadian Mathematical Society 1994

References

1. Azencott, R., Espaces de Poisson des groupes localement compacts, Lecture Notes in Math. 148, Springer, Berlin, 1970.Google Scholar
2. Derriennic, Y., Lois zéro ou deux pour les processus de Markov. Applications aux marches aléatoires, Ann. Inst. H. Poincaré 12(1976), 111–129.Google Scholar
3. Derriennic, Y. and Lin, M., Sur la tribu asymptotique des marches aléatoires sur les groupes, Publ. Séminaires Math., Inst. Rech. Math. Rennes, 1983, 1–6.Google Scholar
4. Frey, A. H., Studies in amenable semigroups, Thesis, University of Washington, Seattle, 1960.Google Scholar
5. Greenleaf, P. F., Invariant means on topological groups and their applications, Van Nostrand, New York, 1969.Google Scholar
6. Guivarc'h, Y., Croissance polynômiale et périodes des fonctions harmoniques, Bull. Soc. Math. France 101(1973), 333–379.Google Scholar
7. Heyer, H., Probability measures on locally compact groups, Springer, Berlin, 1977.Google Scholar
8. Jaworski, W., Strong approximate transitivity, polynomial growth, and spread out random walks on locally compact groups, Pacific J. Math., in press.Google Scholar
9. Jenkins, J. W., Amenable subsemigroups of a locally compact group, Proc. Amer. Math. Soc. 25(1970), 766–770.Google Scholar
10. Jenkins, J. W., Følner's condition for exponentially bounded groups, Math. Scand. 35(1974), 165–174.Google Scholar
11. Jenkins, J. W., Growth of connected locally compact groups, J. Funct. Anal. 12(1973), 113–127.Google Scholar
12. Kaimanovich, V. A. and Vershik, A. M., Random walks on discrete groups: boundary and entropy, Ann. Probab. 11(1983), 457–490.Google Scholar
13. Paterson, A. L. T., Amenability, Amer. Math. Soc, Providence, Rhode Island, 1988.Google Scholar
14. Pier, J.-P., Amenable locally compact groups, Wiley, New York, 1984.Google Scholar
15. Rosenblatt, J. M., Invariant measures and growth conditions, Trans. Amer. Math. Soc. 193(1974), 33–53.Google Scholar
16. Rosenblatt, J., Ergodic and mixing random walks on locally compact groups, Math. Ann. 257(1981), 31–42.Google Scholar