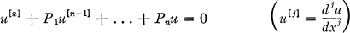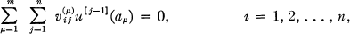Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
1964.
Discrete and Continuous Boundary Problems.
Vol. 8,
Issue. ,
p.
481.
Cole, Randal H.
1964.
General boundary conditions for an ordinary linear differential system.
Transactions of the American Mathematical Society,
Vol. 111,
Issue. 3,
p.
521.
Cole, R. H.
1965.
The Two-Point Boundary Problem.
The American Mathematical Monthly,
Vol. 72,
Issue. 7,
p.
701.
Kelman, Robert B.
Marsh, Donald J.
and
Howard, Henry C.
1966.
Nonmonotonicity of Solutions of Linear Differential Equations Occurring in the Theory of Urine Formation.
SIAM Review,
Vol. 8,
Issue. 4,
p.
463.
Zettl, Anton
1968.
Adjoint and Self-Adjoint Boundary Value Problems with Interface Conditions.
SIAM Journal on Applied Mathematics,
Vol. 16,
Issue. 4,
p.
851.
Krall, Allan M
1968.
Differential operators and their adjoints under integral and multiple point boundary conditions.
Journal of Differential Equations,
Vol. 4,
Issue. 3,
p.
327.
Butuzov, V. F.
Vasil’eva, A. B.
and
Fedoryuk, M. V.
1970.
Mathematical Analysis.
p.
1.
Green, Gary B.
and
Krall, A. M.
1971.
Linear differential systems with infinitely many boundary points.
Annali di Matematica Pura ed Applicata,
Vol. 91,
Issue. 1,
p.
53.
Freiling, Gerhard
1980.
Regul�re Eigenwertprobleme mit Mehrpunkt-Integral-Randbedingungen.
Mathematische Zeitschrift,
Vol. 171,
Issue. 2,
p.
113.
Mennicken, Reinhard
1983.
Banach Space Theory and its Applications.
Vol. 991,
Issue. ,
p.
156.
Mennicken, Reinhard
1984.
Functional Analysis, Holomorphy and Approximation Theory II.
Vol. 86,
Issue. ,
p.
203.
Möller, Manfred
1987.
Expansion theorems for Birkhoff-regular differential-boundary operators.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 107,
Issue. 3-4,
p.
349.
Krall, Allan M
1989.
Asymptotic stability of the Euler-Bernoulli beam with boundary control.
Journal of Mathematical Analysis and Applications,
Vol. 137,
Issue. 1,
p.
288.
SHIFMAN, JEFFREY J.
1993.
Lyapunov functions and the control of the Euler-Bernoulli beam.
International Journal of Control,
Vol. 57,
Issue. 4,
p.
971.
Langer, Heinz
Mennicken, Reinhard
and
Möller, Manfred
1993.
Expansion of Analytic Functions in Series of Floquet Solutions of First Order Differential Systems.
Mathematische Nachrichten,
Vol. 162,
Issue. 1,
p.
279.
Tretter, Christiane
2000.
Spectral Problems for Systems of Differential Equationsy′ +A0y = λA1y with λ-Polynomial Boundary Conditions.
Mathematische Nachrichten,
Vol. 214,
Issue. 1,
p.
129.
2003.
Non-Self-Adjoint Boundary Eigenvalue Problems.
Vol. 192,
Issue. ,
p.
475.
Behncke, Horst
and
Hinton, Don
2010.
Two singular point linear Hamiltonian systems with an interface condition.
Mathematische Nachrichten,
Vol. 283,
Issue. 3,
p.
365.