No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
Consider the elliptic quasilinear problem:
1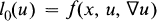
in Rn, n ≧ 3, where
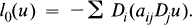
We are interested in establishing sufficient conditions on f for the existence of positive solutions u(x) with specified behaviour at ∞. Of special interest to us are criteria which guarantee that u(x) decays at least as fast as |x|−α for some α ≧ 0, given below, in the case f(x, u, ∇u) contains terms of type
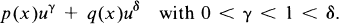
That is: f is of mixed sublinear-super linear type. Our main result is Theorem 3 below which explicitly states sufficient conditions for the existence of such solutions.