Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T02:19:19.835Z Has data issue: false hasContentIssue false
  • English
  • Français

Euler's Criterion for Quintic Nonresidues

Published online by Cambridge University Press:  20 November 2018

S. A. Katre  and
A. R. Rajwade
S. A. Katre
Affiliation:
Panjab University, Chandigarh, India
A. R. Rajwade
Affiliation:
Panjab University, Chandigarh, India
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let e be an integer ≧ 2, and p a prime = 1 (mod e). Euler's criterion states that for D ∊ Z,

(1.1)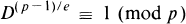

if and only if D is an e-th power residue (mod p). If D is not an e-th power (mod p), one has

(1.2)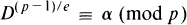

for some e-th root α(≠1) of unity (mod p). Sometimes expressions for roots of unity (mod p) can be given in terms of quadratic partitions of p. For example,

(1.3)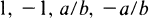

are the four distinct fourth roots of unity (mod p) for a prime p ≡ 1 (mod 4) in terms of a solution (a, b) of the diophantine system

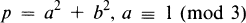
(a, b unique), whereas for p ≡ 1 (mod 3), a solution (L, M) of the system

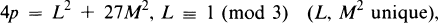
gives

(1.4)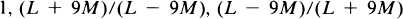

as the three distinct cuberoots of unity (mod p).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 37 , Issue 5 , 01 October 1985 , pp. 1008 - 1024
Copyright
Copyright © Canadian Mathematical Society 1985

References

1. Dickson, L. E., Cyclotomy, higher congruences, and Warings problem, Amer. J. Math. 57 (1935), 391–424.Google Scholar
2. Hudson, R. H. and Williams, K. S., Extensions of theorems of Cunningham-A igner and Hasse-Evans, Pacific J. Math. 104 (1983), 111–132.Google Scholar
3. Lehmer, E., The quintic character of 2 and 3, Duke Math. J. 18 (1951), 11–18.Google Scholar
4. Lehmer, E., On Euler's criterion, J. Austral. Math. Soc. (1959/61), Part I, 64–70.Google Scholar
5. Lehmer, E., On the divisors of the discriminant of the period equation, Amer. J. Math. 90 (1968), 375–379.Google Scholar
6. Leonard, P. A. and Williams, K. S., The cyclotomic numbers of order seven, Proc. Amer. Math. Soc. 51 (1975), 295–300.Google Scholar
7. Leonard, P. A. and Williams, K. S., The cyclotomic numbers of order eleven, Acta Arith. 26 (1975), 365–383.Google Scholar
8. Muskat, J. B., On the solvability of xe ≡ e(mod p), Pacific J. Math. 14 (1964), 257–260.Google Scholar
9. Parnami, J. C., Agrawal, M. K. and Rajwade, A. R., Jacobi sums and cyclotomic numbers, Acta Arith. 41 (1982), 1–13.Google Scholar
10. Williams, K. S., On Euler's criterion for cubic nonresidues, Proc. Amer. Math. Soc. 49 (1975), 277–283.Google Scholar
11. Williams, K. S., Explicit criteria for quintic residuacity, Math. Comp. 30 (1976), 847–853.Google Scholar
12. Williams, K. S., On Euler's criterion for quintic nonresidues, Pacific J. Math. 57 (1975), 543–550.Google Scholar