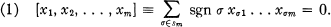Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Guy, Richard K.
1975.
Monthly Research Problems, 1969–75.
The American Mathematical Monthly,
Vol. 82,
Issue. 10,
p.
995.
1980.
Polynomial Identities in Ring Theory.
Vol. 84,
Issue. ,
p.
341.
Pouzet, M.
1985.
Graphs and Order.
p.
592.
1991.
Eulerian Graphs and Related Topics.
Vol. 50,
Issue. ,
p.
A.1.
Giambruno, Antonio
Ioppolo, Antonio
and
Martino, Fabrizio
2016.
Standard polynomials and matrices with superinvolutions.
Linear Algebra and its Applications,
Vol. 504,
Issue. ,
p.
272.
Bessades, D. C. L.
dos Santos, R. B.
and
Vieira, A. C.
2022.
Minimal degree of standard identities of matrix algebras with symplectic graded involution.
International Journal of Algebra and Computation,
Vol. 32,
Issue. 01,
p.
47.