Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T00:26:12.777Z Has data issue: false hasContentIssue false
  • English
  • Français

The Eta Invariant and Equivariant SpinC Bordism for Spherical Space form Groups

Published online by Cambridge University Press:  20 November 2018

Peter B. Gilkey
Peter B. Gilkey*
Affiliation:
University of Oregon, Eugene, Oregon
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A finite group G is a spherical space form group if it admits a fixed point free representation τ:G → U(k) for some k; for the remainder of this paper, we assume G is such a group. The eta invariant of Atiyah et al [2] defines Q/Z valued invariants of equivariant bordism. In [6], we showed the eta invariant completely detects the reduced equivariant unitary bordism groups 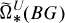and completely detects all but the 2-primary part of the reduced equivariant SpinC bordism groups 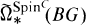. The coefficient ring 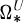is without torsion; all the torsion in 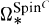is of order 2. The prime 2 plays a distinguished role in the discussion of equivariant SpinC bordism and 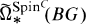is quite different from 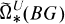at the prime 2. Let ker*(η, G) denote the kernel of all eta invariants and let ker*(SW, G) denote the kernel of the Z2-equivariant Stiefel-Whitney numbers (see Section 1 for details). Then:

THEOREM 0.1. Let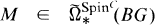. If M = ker*(η, G) ∩ ker*(SW, G), M = 0.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 40 , Issue 2 , 01 April 1988 , pp. 392 - 428
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Anderson, D. W., Brown, E. H. and Peterson, F. P., Spin cobordism, Bulletin of the American Mathematics Society 72 (1966), 257–260.Google Scholar
2. Atiyah, M. F., Patodi, V. K. and Singer, I. M., Spectral asymmetry and Riemannian geometry I, Math. Proc. Camb. Phil. Soc. 77 (1975), 43–69. II, Math. Proc. Camb. Phil. Soc. 78 (1975), 405–432. III, Math. Proc. Camb. Phil. Soc. 79 (1976), 71–99.Google Scholar
3. Bahri, A. and Gilkey, P., The eta invariant, PinC bordism, and equivariant SpinC bordism for cyclic 2-groups, Pacific Journal Math 128 (1987), 1–24.Google Scholar
4. Bahri, A. and Gilkey, P., PinC bordism and equivariant SpinC bordism for cyclic 2-groups, Proceedings of AMS 99(1987), 380–382.Google Scholar
5. Conner, P. E. and Floyd, E. E., Differentiable periodic maps (Springer-Verlag, (1964).Google Scholar
6. Gilkey, P., The eta invariant and equivariant unitary bordism for spherical space form groups (to appear in Compositio Math).Google Scholar
7. Gilkey, P., The eta invariant and the K-theory of spherical space forms, Inventiones Math 76 (1984), 421–453.Google Scholar
8. Gilkey, P. Invariance theory, the heat equation, and the Atiyah-Singer index theorem (Publish or Perish Press, 1985).Google Scholar
9. Johnson, D. and Wilson, S., Projective dimension and Brown-Peterson homology, Topology 12 (1973), 327–353.Google Scholar
10. Landweber, P., Complex bordism of classifying spaces, Proceedings of the American Mathematical Society 27 (1971), 175–179.Google Scholar
11. Stong, R. E., Notes on cobordism (Princeton University Press, 1968).Google Scholar
12. Wolf, J. A., Spaces of constant curvature, 5th ed (Publish or Perish Press, 1984).Google Scholar