Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-27T19:35:35.004Z Has data issue: false hasContentIssue false
  • English
  • Français

Estimates of Hausdorff Dimension for the Non-Wandering Set of an Open Planar Billiard

Published online by Cambridge University Press:  20 November 2018

Robert Kenny
Robert Kenny*
Affiliation:
The University of Western Australia, School of Mathematics & Statistics (M019), 35 Stirling Highway, Crawley, WA 6009, Australia e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The billiard flow in the plane has a simple geometric definition; the movement along straight lines of points except where elastic reflections are made with the boundary of the billiard domain. We consider a class of open billiards, where the billiard domain is unbounded, and the boundary is that of a finite number of strictly convex obstacles. We estimate the Hausdorff dimension of the nonwandering set 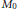${{M}_{0}}$ of the discrete time billiard ball map, which is known to be a Cantor set and the largest invariant set. Under certain conditions on the obstacles, we use a well-known coding of 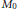${{M}_{0}}$ [Mor91] and estimates using convex fronts related to the derivative of the billiard ball map [Sto03] to estimate the Hausdorff dimension of local unstable sets. Consideration of the local product structure then yields the desired estimates, which provide asymptotic bounds on the Hausdorff dimension's convergence to zero as the obstacles are separated.

Keywords

37D5037C4528A78
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 56 , Issue 1 , 01 February 2004 , pp. 115 - 133
Copyright
Copyright © Canadian Mathematical Society 2004

References

[BSC90] Bunimovich, L. A., Sinaĭ, Ya. G. and Chernov, N. I., Markov partitions for two-dimensional hyperbolic billiards. Uspekhi Mat. Nauk 3(273) 45(1990), 97–134, 221.Google Scholar
[Bun89] Bunimovich, L. A., Dynamical systems of hyperbolic type with singularities. In: Dynamical systems, II, Springer-Verlag, Berlin, 1989, 151–178.Google Scholar
[dM73] de Melo, W., Structural stability of diffeomorphisms on two-manifolds. Invent. Math. 21(1973), 233–246.Google Scholar
[Edg90] Edgar, Gerald A., Measure, topology, and fractal geometry. Springer-Verlag, New York, 1990.Google Scholar
[Ika88] Ikawa, Mitsuru, Decay of solutions of the wave equation in the exterior of several convex bodies. Ann. Inst. Fourier (Grenoble) 38(1988), 113–146.Google Scholar
[LM96] Lopes, Artur and Markarian, Roberto, Open billiards: invariant and conditionally invariant probabilities on Cantor sets. SIAM J. Appl. Math. 56(1996), 651–680.Google Scholar
[Mar54] Marstrand, J. M., The dimension of Cartesian product sets. Proc. Cambridge Philos. Soc. 50(1954), 198–202.Google Scholar
[Mat95] Pertti Mattila, Geometry of sets and measures in Euclidean spaces. Cambridge University Press, Cambridge, 1995.Google Scholar
[MM83] McCluskey, Heather and Manning, Anthony, Hausdorff dimension for horseshoes. Ergodic Theory Dynam. Systems 3(1983), 251–260.Google Scholar
[Mor91] Morita, Takehiko, The symbolic representation of billiards without boundary condition. Trans. Amer.Math. Soc. 325(1991), 819–828.Google Scholar
[Pix83] Pixton, Dennis, Markov neighborhoods for zero-dimensional basic sets. Trans. Amer. Math. Soc. 279(1983), 431–462.Google Scholar
[PS92] Petkov, Vesselin M. and Stoyanov, Luchezar N., Geometry of reècting rays and inverse spectral problems. John Wiley & Sons Ltd., Chichester, 1992.Google Scholar
[PT93] Palis, Jacob and Takens, Floris, Hyperbolicity and sensitive chaotic dynamics at homoclinic bifurcations. Cambridge University Press, Cambridge, 1993.Google Scholar
[PV88] Palis, J. and Viana, M., On the continuity of Hausdorff dimension and limit capacity for horseshoes. In: Dynamical systems (Valparaiso, 1986), Springer, Berlin, 1988, 150–160.Google Scholar
[Rob75] Robinson, R. Clark, Structural stability of C 1 flows. Lecture Notes in Math. 468, Springer, Berlin, 1975, 262–277.Google Scholar
[Sin70] Sinaĭ, Ja. G., Dynamical systems with elastic reèctions. Ergodic properties of dispersing billiards. Uspehi Mat. Nauk 2(152) 25(1970), 141–192.Google Scholar
[Sin79] Sinai, Ya. G., Development of Krylov's ideas. Princeton University Press, Princeton, N.J., 1979. An addendum to the book. Works on the foundations of statistical physics. by N. S. Krylov, Princeton Series in Physics.Google Scholar
[Sjö90] Sjöstrand, Johannes, Geometric bounds on the density of resonances for semiclassical problems. Duke Math. J. 60(1990), 1–57.Google Scholar
[Sto03] Stoyanov, Luchezar N., A sharp asymptotic for the lengths of certain scattering rays in the exterior of two convex domains. Asymptot. Anal. 35(2003), 235–255.Google Scholar
[Tri82] Tricot, Claude Jr., Two definitions of fractional dimension. Math. Proc. Cambridge Philos. Soc. 91(1982), 57–74.Google Scholar