Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-24T04:48:20.552Z Has data issue: false hasContentIssue false
  • English
  • Français

Estimates of Hausdorff Dimension for Non-wandering Sets of Higher Dimensional Open Billiards

Published online by Cambridge University Press:  20 November 2018

Paul Wright
Paul Wright*
Affiliation:
Mathematics Department, University of Western Australia, Perth, Western Australia, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This article concerns a class of open billiards consisting of a finite number of strictly convex, non-eclipsing obstacles $K$. The non-wandering set 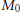${{M}_{0}}$ of the billiard ball map is a topological Cantor set, and its Hausdorff dimension has been previously estimated for billiards in ${{\mathbb{R}}^{2}}$ using well-known techniques. We extend these estimates to billiards in 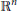${{\mathbb{R}}^{n}}$ and make various refinements to the estimates. These refinements also allow improvements to other results. We also show that in many cases, the non-wandering set is confined to a particular subset of 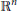${{\mathbb{R}}^{n}}$ formed by the convex hull of points determined by period 2 orbits. This allows more accurate bounds on the constants used in estimating Hausdorff dimension.

Keywords

37D2037D40dynamical systemsbilliardsdimensionHausdorff
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 65 , Issue 6 , 01 December 2013 , pp. 1384 - 1400
Copyright
Copyright © Canadian Mathematical Society 2013

References

[BCST] Bálint, P., Chernov, N., Szász, D., and P. Tóth, I., Geometry of multi-dimensional dispersing billiards. Geometric methods in dynamics. I. Astérisque 286(2003), 119–150.Google Scholar
[B] Barreira, L. M., A non-additive thermodynamic formalism and applications to dimension theory of hyperbolic dynamical sytems. Ergodic Theory Dynam. Systems 16(1996), no. 5, 871–927. http://dx.doi.org/10.1017/S0143385700010117 Google Scholar
[Ch] Chernov, N. and Markarian, R., Chaotic billiards. Mathematical Surveys and Monographs, 127, American Mathematical Society, Providence, RI, 2006.Google Scholar
[Ed] Edgar, G. A., Measure, topology and fractal geometry. Undergraduate Texts in Mathematics, Springer-Verlag, New York, 1990.Google Scholar
[Fa] Falconer, K., Fractal geometry. Mathematical foundations and applications. Second ed., John Wiley and Sons, Hoboken, NJ, 2003.Google Scholar
[H] Hassleblatt, B., Regularity of the Anosov splitting II. Ergodic Theory Dynam. Systems 17(1997), no. 1, 169–172. http://dx.doi.org/10.1017/S0143385797069757 Google Scholar
[HS] Hasselblatt, B. and Schmeling, J., Dimension product structure of hyperbolic sets. Electon. Res. Announc. Amer. Math. Soc. 10(2004), 88–96. http://dx.doi.org/10.1090/S1079-6762-04-00133-7 Google Scholar
[KH] Katok, A. and Hasselblatt, B., Introduction to the modern theory of dynamical systems. Encyclopedia of Mathematics and its Applications, 54, Cambridge University Press, Cambridge, 1995.Google Scholar
[Ke] Kenny, R., Estimates of Hausdorff dimension for the non-wandering set of an open planar billiard. Canad. J. Math. 56(2004), no. 1, 115–133. http://dx.doi.org/10.4153/CJM-2004-006-8 Google Scholar
[P] Pesin, Y., Dimension theory in dynamical systems. Contemporary views and applications. Chicago Lectures in Mathematics, University of Chicago Press, Chicago, IL, 1997.Google Scholar
[S1] Sinai, Y. G., Dynamical systems with elastic reflections. Ergodic properties of dispersing billiards. (Russian) Uspehi Mat. Nauk 25(1970), no. 2, 141–192.Google Scholar
[S2] Sinai, Y. G., Development of Krylov's ideas. In: Works on the foundations of statistical physics, Princeton Serier in Physics, Princeton University Press, Princeton, NJ, 1979, pp. 239–281.Google Scholar
[SCh] Sinai, Y. G. and Chernov, N. I., Ergodic properties of some systems of two-dimensional disks and three-dimensional balls. (Russian) Uspekhi Mat. Nauk 42(1987), no. 3, 153–174, 256 Google Scholar
[Sjö] Sjöstrand, J., Geometric bounds on the density of resonances for semiclassical problems. Duke Math. J. 60(1990), no. 1, 1–57. http://dx.doi.org/10.1215/S0012-7094-90-06001-6 Google Scholar
[Sto1] Stoyanov, L., An estimate from above of the number of periodic orbits for semi-dispersed billiards. Commun. Math. Phys. 124(1989), no. 2, 217–227. http://dx.doi.org/10.1007/BF01219195 Google Scholar
[Sto2] Stoyanov, L., Spectrum of the Ruelle operator and exponential decay of correlations for open billiard flows. Amer. J. Math. 123(2001), no. 4, 715–759. http://dx.doi.org/10.1353/ajm.2001.0029 Google Scholar
[Sto3] Stoyanov, L., Non-integrability of open billiard flows and Dolgopyat-type estimates. Ergodic Theory Dynam. Systems 32(2012), no. 1, 295–313. http://dx.doi.org/10.1017/S0143385710000933 Google Scholar