Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-26T17:26:19.105Z Has data issue: false hasContentIssue false
  • English
  • Français

Essentially Convexoid Operators

Published online by Cambridge University Press:  20 November 2018

Takayuki Furuta
Takayuki Furuta*
Affiliation:
Hirosaki University, Hirosaki, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let H be a separable complex Hilbert space and let B(H) denote the algebra of all bounded linear operators on H. Let π be the quotient mapping from B(H) onto the Calkin algebra B(H)/K(H), where K(H) denotes all compact operators on B(H). An operator T ∈ B(H) is said to be convexoid[14] if the closure 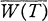of its numerical range W(T) coincides with the convex hull co σ(T) of its spectrum σ(T). T ∈ B(H) is said to be essentially normal, essentially G1, or essentially convexoid if π(T) is normal, G1 or convexoid in B(H)/K(H) respectively.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 2 , 01 April 1981 , pp. 257 - 274
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Berberian, S. K., Condition on an operator implying Rea(T) = <r(ReT), Trans. Amer. Math. Soc. 154 (1971), 267–272.Google Scholar
2. Berberian, S. K., The Weyl spectrum of an operator, Indiana University Math. J. 20 (1970), 529–544.Google Scholar
3. Chui, C. K., Smith, P. W., Ward, J. D. and Legg, D. A., On a question of 01sen concerning compact perturbations, Notices Amer. Math. Soc. 23 (1976), 164.Google Scholar
4. Douglas, R. G., Banach algebra techniques in operator theory (Academic Press, New York, 1972).Google Scholar
5. Fillmore, P. A., Stampfli, J. G. and Williams, J. P., On the essential numerical range, the essential spectrum and a problem ofHalmos, Acta Sci. Math. 33 (1972), 179–192.Google Scholar
6. Fujii, M., n some examples of non-normal operators, II, Proc. Japan Acad. 1+9 (1973), 118–123.Google Scholar
7. Fujii, M. and Nakamoto, R., On a conjecture of Luecke, Math. Japonicae 22 (1977), 79–82.Google Scholar
8. Furuta, T., A note on two inequalities correlated to unitary p-dilations, Proc. Japan Acad. 45 (1969), 561–564.Google Scholar
9. Furuta, T., Some theorems on unitary p-dilations of Sz.-Nagy and Foias, Acta Sci. Math. 33 (1972), 119–122.Google Scholar
10. Furuta, T., Some characterizations of convexoid operators, Rev. Roum. Math. Pures et Appl. 18 (1973), 893–900.Google Scholar
11. Furuta, T., Relations between generalized growth conditions and several classes of convexoid operators, Can. J. Math. 5 (1977), 1010–1030.Google Scholar
12. Furuta, T., Convexoid operators and generalized growth conditions associated with unitary p-dilations of Sz.-Nagy and Foias, Acta Sci. Math. 40 (1978), 53–61.Google Scholar
13. Furuta, T. and Nakamoto, R., On the numerical range of an operator, Proc. Japan Acad. 47 (1971), 279–284.Google Scholar
14. Halmos, P. R., A Hilbert space problem book (Van Nostrand, Princeton, 1967).Google Scholar
15. Holbrook, J., On the power bounded operators of Sz.-Nagy and C. Foias, Acta Sci. Math. 29 (1968), 299–310.Google Scholar
16. Lin, C.-S., On a family of generalized numerical ranges, Can. J. Math. 26 (1974), 678–685.Google Scholar
17. Luecke, G. R., A class of operators on Hilbert space, Pacific J. Math. 41 (1971) 153–156.Google Scholar
18. Luecke, G. R., Essentially (Gi) operators and essentially convexoid operators on Hilbert space, Illinois J. Math. 19 (1975), 389–399.Google Scholar
19. Orland, G. H., On a class of operators, Proc. Amer. Math. Soc. 15 (1964), 75–79.Google Scholar
20. Patel, S. M., A note on a class of operators, Math. Nachr. 78 (1976), 357–361.Google Scholar
21. Patel, S. M., On some classes of operators associated with operator radii of Holbrook, 39th Conf. of Indian Math. Soc. (1973).Google Scholar
22. Patel, S. M., On generalized numerical range, Pacific J. Math. 66 (1976), 235–241.Google Scholar
23. Salinas, N., Reducing essential eigenvalues, Duke Math. J. 40 (1973), 561–580.Google Scholar
24. Salinas, N., Operators with essentially disconnected spectrum, Acta Sci. Math. 33 (1972), 193–205.Google Scholar
25. Stampfli, J. G., Compact perturbations, normal eigenvalues and a problem of Salinas, J. London Math. Soc. 2 (1974), 165–175.Google Scholar
26. Stampfli, J. G. and Williams, J. P., Growth conditions and numerical range in a Banach algebra, Tohoku Math. J. 20 (1968), 417–424.Google Scholar
27. -Nagy, B.Sz. and Foias, C., On certain classes of power bounded operators in Hilbert space, Acta Sci. Math. 27 (1966), 17–25.Google Scholar
28. -Nagy, B.Sz. and Foias, C., Harmonic analysis of operators on Hilbert space (North Holland, 1970).Google Scholar
29. Whitley, R., The spectral theorem for a normal operator, Amer. Math. Monthly 75 (1968), 856–861.Google Scholar