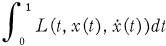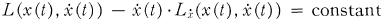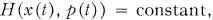Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Treiman, Jay S.
1983.
Characterization of Clarke's tangent and normal cones in finite and infinite dimensions.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 7,
Issue. 7,
p.
771.
May, Helge-Otmar
1984.
Generalized variational principles and nondifferentiable potentials in analytical mechanics.
Journal of Mathematical Physics,
Vol. 25,
Issue. 3,
p.
491.
Borisovich, Yu. G.
Gel'man, B. D.
Myshkis, A. D.
and
Obukhovskii, V. V.
1984.
Multivalued mappings.
Journal of Soviet Mathematics,
Vol. 24,
Issue. 6,
p.
719.
Treiman, Jay S.
1986.
Clarke’s gradients and epsilon-subgradients in Banach spaces.
Transactions of the American Mathematical Society,
Vol. 294,
Issue. 1,
p.
65.
Clarke, Frank H.
and
Watkins, Gavin G.
1986.
Necessary conditions, controllability and the value function for differential-difference inclusions.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 10,
Issue. 11,
p.
1155.
Treiman, J.S.
1986.
Generalized gradients and paths of descent.
Optimization,
Vol. 17,
Issue. 2,
p.
181.
Ioffe, A. D.
and
Rockafellar, R. T.
1996.
The Euler and Weierstrass conditions for nonsmooth variational problems.
Calculus of Variations and Partial Differential Equations,
Vol. 4,
Issue. 1,
p.
59.
Boito, Paola
and
Dedieu, Jean-Pierre
2010.
The Condition Metric in the Space of Rectangular Full Rank Matrices.
SIAM Journal on Matrix Analysis and Applications,
Vol. 31,
Issue. 5,
p.
2580.
Yunt, Kerim
2012.
The Impulsive Action Integral for Rigid-Body Mechanical Systems With Impacts.
Journal of Computational and Nonlinear Dynamics,
Vol. 7,
Issue. 3,
Beltrán, Carlos
Dedieu, Jean-Pierre
Malajovich, Gregorio
and
Shub, Mike
2012.
Convexity Properties of the Condition Number II.
SIAM Journal on Matrix Analysis and Applications,
Vol. 33,
Issue. 3,
p.
905.
Dolgopolik, Maksim
2021.
Constrained nonsmooth problems of the calculus of variations.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 27,
Issue. ,
p.
79.
Fominyh, Alexander
2022.
Mathematical Optimization Theory and Operations Research.
Vol. 13367,
Issue. ,
p.
34.
Fominyh, A. V.
2023.
The subdifferential descent method in a nonsmooth variational problem.
Optimization Letters,
Vol. 17,
Issue. 3,
p.
675.