Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T01:13:09.494Z Has data issue: false hasContentIssue false
  • English
  • Français

Equivariant Embeddings into Smooth Toric Varieties

Published online by Cambridge University Press:  20 November 2018

Jürgen Hausen
Jürgen Hausen*
Affiliation:
Fachbereich Mathematik und Statistik, Universität Konstanz, 78457 Konstanz, Germany, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

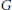We characterize embeddability of algebraic varieties into smooth toric varieties and prevarieties. Our embedding results hold also in an equivariant context and thus generalize a well-known embedding theorem of Sumihiro on quasiprojective $G$-varieties. The main idea is to reduce the embedding problem to the affine case. This is done by constructing equivariant affine conoids, a tool which extends the concept of an equivariant affine cone over a projective 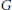$G$-variety to a more general framework.

Keywords

14E2514C2014L3014M25
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 54 , Issue 3 , 01 June 2002 , pp. 554 - 570
Copyright
Copyright © Canadian Mathematical Society 2002

References

[1] A’Campo-Neuen, A. and Hausen, J., Quasi-projective reduction of toric varieties. Math. Z. (4) 233 (2000), 697–708.Google Scholar
[2] A’Campo-Neuen, A. and Hausen, J., Toric prevarieties and subtorus actions. Geom. Dedicata, mathAG/9912229, to appear.Google Scholar
[3] A’Campo-Neuen, A. and Hausen, J. and Schröer, S., Quotient presentations and homogeneous coordinates for toric varieties. Math. Nachr., math.AG/0005083, to appear.Google Scholar
[4] Białynicki-Birula, A., Finiteness of the number of maximal open subsets with good quotients. Transformation Groups (4) 3 (1998), 301–319.Google Scholar
[5] Borelli, M., Divisorial varieties. Pacific J. Math. 13 (1963), 375–388.Google Scholar
[6] Cox, D., The homogeneous coordinate ring of a toric variety. J. Algebraic Geom. 4 (1995), 17–51.Google Scholar
[7] Fulton, W., Introduction to Toric Varieties. Princeton University Press, Princeton, 1993.Google Scholar
[8] Hausen, J., On Włodarczyk's embedding theorem. Internat. J. Math. (6) 11 (2000), 811–836.Google Scholar
[9] Hausen, J. and Schröer, S., On embeddings into toric prevarieties. Preprint, math.AG/0002046.Google Scholar
[10] Humphreys, J. E., Linear Algebraic Groups. Graduate Texts in Math., Springer, Berlin-New York, 1975.Google Scholar
[11] Kajiwara, T., The functor of a toric variety with enough invariant effective cartier divisors. Tôhoku Math. J. (1) 50 (1998), 139–157.Google Scholar
[12] Knop, F., Kraft, H., Luna, D., Vust, T., Local properties of algebraic group actions. In: Algebraische Transformationsgruppen und Invariantentheorie, DMV Seminar Band 13. Birkhäuser, Basel, 1989.Google Scholar
[13] Sumihiro, H., Equivariant completion. J. Math. Kyoto Univ. 14 (1974), 1–28.Google Scholar
[14] Świeçicka, J., A Combinatorial construction of sets with good quotients by an action of a reductive group. Colloq. Math. (1) 87 (2001), 85–102.Google Scholar
[15] Włodarczyk, J., Embeddings in toric varieties and prevarieties. J. Algebraic Geom. 2 (1993), 705–726.Google Scholar