Le problème de la construction d'enveloppes d'holomorphie globales ou d'enveloppes polynomialement convexes n'a été que très peu abordé et peu d'exemples explicites sont connus. Il semble donc qu'il soit intéressant de se limiter d'abord au calcul d'enveloppes d'ensembles homogènes, par l'action d'un groupe agissant par transformations holomorphes. C'est le cas des sphères unité de Cn, des polytores par exemple. En s'inspirant des actions de groupes discutés par Ehrenpreis [2] ou par Hua [3], nous considérons ici l'action des groupes SU(2) et U(2) sur C3 identifié à l'ensemble des matrices symétriques complexes 2 × 2. L'action de SU(2) sur C3 est en fait l'action canonique de SU(2) sur une famille de quadriques 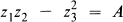dégénérant vers la quadrique singulière lorsque A tends vers 0. L'étude des orbites est équivalente à l'étude des équations de Cauchy Riemann sur SU(2), invariantes à gauche. Le spectre de l'algèbre des fonctions annulant une telle équation sur SU(2), qui sont invariantes par l'application antipodale est alors un domaine d'holomorphie de l'une de ces quadriques qui est d'ailleurs topologiquement non trivial.