No CrossRef data available.
Article contents
The epsilon constant conjecture for higher dimensional unramified twists of 
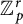${\mathbb Z}_p^r$(1)
Published online by Cambridge University Press: 29 June 2021
Abstract
Let 
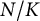$N/K$
be a finite Galois extension of p-adic number fields, and let 
$\rho ^{\mathrm {nr}} \colon G_K \longrightarrow \mathrm {Gl}_r({{\mathbb Z}_{p}})$
be an r-dimensional unramified representation of the absolute Galois group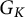 
$G_K$
, which is the restriction of an unramified representation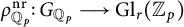 
$\rho ^{\mathrm {nr}}_{{{\mathbb Q}}_{p}} \colon G_{{\mathbb Q}_{p}} \longrightarrow \mathrm {Gl}_r({{\mathbb Z}_{p}})$
. In this paper, we consider the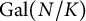 
$\mathrm {Gal}(N/K)$
-equivariant local 
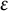$\varepsilon $
-conjecture for the p-adic representation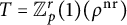 
$T = \mathbb Z_p^r(1)(\rho ^{\mathrm {nr}})$
. For example, if A is an abelian variety of dimension r defined over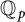 
${{\mathbb Q}_{p}}$
with good ordinary reduction, then the Tate module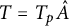 
$T = T_p\hat A$
associated to the formal group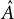 
$\hat A$
of A is a p-adic representation of this form. We prove the conjecture for all tame extensions 
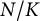$N/K$
and a certain family of weakly and wildly ramified extensions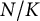 
$N/K$
. This generalizes previous work of Izychev and Venjakob in the tame case and of the authors in the weakly and wildly ramified case.
Keywords
MSC classification
Secondary:
11S40: Zeta functions and $L$-functions
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2021
References
Benois, D. and Berger, L., Théorie d’Iwasawa des représentations cristallines. II. Comment. Math. Helv. 83(2008), no. 3, 603–677.CrossRefGoogle Scholar
Bley, W. and Cobbe, A., Equivariant epsilon constant conjectures for weakly ramified extensions. Math. Z. 283(2016), nos. 3–4, 1217–1244.CrossRefGoogle Scholar
Bley, W. and Cobbe, A.,
The equivariant local
$\varepsilon$
-constant conjecture for unramified twists of ℤ
p
(1). Acta Arith. 178(2017), no. 4, 313–383.CrossRefGoogle Scholar
$\varepsilon$
-constant conjecture for unramified twists of ℤ
p
(1). Acta Arith. 178(2017), no. 4, 313–383.CrossRefGoogle ScholarBley, W. and Wilson, S. M. J.,
Computations in relative algebraic
$K$
-groups
. LMS J. Comput. Math. 12(2009), 166–194.CrossRefGoogle Scholar
$K$
-groups
. LMS J. Comput. Math. 12(2009), 166–194.CrossRefGoogle ScholarBloch, S. and Kato, K.,
L-functions and Tamagawa numbers of motives
. In: The Grothendieck Festschrift. Vol. I, Cartier, P., Illusie, L., Katz, N., Laumon, G., Manin, Y., Ribet, K. (eds.), Progress in Mathematics, 86, Birkhäuser Boston, Boston, MA, 1990, pp. 333–400.Google Scholar
Breuning, M., Equivariant local epsilon constants and étale cohomology. J. London Math. Soc. (2) 70(2004), no. 2, 289–306.Google Scholar
Breuning, M., Equivariant epsilon constants for Galois extensions of number fields and
$p$
-adic fields. Ph.D. thesis, King’s College London, 2004.Google Scholar
$p$
-adic fields. Ph.D. thesis, King’s College London, 2004.Google ScholarBreuning, M. and Burns, D.,
Additivity of Euler characteristics in relative algebraic
$K$
-groups
. Homol Homotopy Appl. 7(2005), no. 3, 11–36.CrossRefGoogle Scholar
$K$
-groups
. Homol Homotopy Appl. 7(2005), no. 3, 11–36.CrossRefGoogle ScholarBurns, D. and Nickel, A., Equivariant local epsilon constants and Iwasawa theory. Work in progress.Google Scholar
Cobbe, A., A representative of
$R\varGamma \left(N,T\right)$
for some unramified twists of
${\mathbb{Z}}_p^r$
. Int. J. Number Theory https://doi.org/10.1142/S1793042121500706
Google Scholar
$R\varGamma \left(N,T\right)$
for some unramified twists of
${\mathbb{Z}}_p^r$
. Int. J. Number Theory https://doi.org/10.1142/S1793042121500706
Google ScholarEllerbrock, N. and Nickel, A., On formal groups and Tate cohomology in local fields. Acta Arith. 182(2018), no. 3, 285–299.CrossRefGoogle Scholar
Fröhlich, A., Formal groups. Lecture Notes in Mathematics, 74, Springer, Berlin and New York, 1968.Google Scholar
Fröhlich, A., Galois module structure of algebraic integers. Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], 1, Springer, Berlin, 1983.CrossRefGoogle Scholar
Hazewinkel, M., Formal groups and applications. Pure and Applied Mathematics, 78, Academic Press, Inc. [Harcourt Brace Jovanovich, Publishers], New York and London, 1978.Google Scholar
Izychev, D. and Venjakob, O., Equivariant epsilon conjecture for 1-dimensional Lubin–Tate groups. J. Théor. Nombres Bordeaux 28(2016), no. 2, 485–521.CrossRefGoogle Scholar
Köck, B., Galois structure of Zariski cohomology for weakly ramified covers of curves. Amer. J. Math. 126(2004), no. 5, 1085–1107.CrossRefGoogle Scholar
Lubin, J. and Rosen, M. I., The norm map for ordinary abelian varieties. J. Algebra 52(1978), no. 1, 236–240.Google Scholar
Martinet, J.,
Character theory and Artin L-functions
. In: Algebraic number fields: L-functions and Galois properties (Proc. Sympos., Univ. Durham, Durham, 1975), Academic Press, London, 1977, pp. 1–87.Google Scholar
Mazur, B., Rational points of abelian varieties with values in towers of number fields. Invent. Math. 18(1972), 183–266.CrossRefGoogle Scholar
Neukirch, J., Algebraic number theory [Algebraische Zahlentheorie]. Springer, Berlin, 1992.Google Scholar
Nickel, A., An equivariant Iwasawa main conjecture for local fields. Preprint, 2018. arXiv:1803.05743.Google Scholar
Pickett, E. J. and Vinatier, S., Self-dual integral normal bases and Galois module structure. Compos. Math. 149(2013), no. 7, 1175–1202.Google Scholar
Silverman, J. H., The arithmetic of elliptic curves. 2nd ed., Graduate Texts in Mathematics, 106, Springer, Dordrecht, 2009.CrossRefGoogle Scholar
Swan, R. G., K-theory of finite groups and orders. Lecture Notes in Mathematics, 149, Springer, Berlin and New York, 1970.CrossRefGoogle Scholar
Washington, L. C., Introduction to cyclotomic fields. 2nd ed., Graduate Texts in Mathematics, 83, Springer, New York, 1997.CrossRefGoogle Scholar