Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T00:48:21.379Z Has data issue: false hasContentIssue false
  • English
  • Français

Epimorphisms From S(X) onto S(Y)

Published online by Cambridge University Press:  20 November 2018

K. D. Magill Jr. ,
P. R. Misra  and
U. B. Tewari
K. D. Magill Jr.
Affiliation:
SUNY at Buffalo, Buffalo, New York
P. R. Misra
Affiliation:
College of Staten Island, Staten Island, New York
U. B. Tewari
Affiliation:
IIT-Kanpur, Kanpur, India
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. Introduction. In this paper, the expression topological space will always mean generated space, that is any T1 space X for which

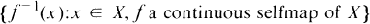
forms a subbasis for the closed subsets of X. This is not at all a severe restriction since generated spaces include all completely regular Hausdorff spaces which contain an arc as well as all 0-dimensional Hausdorff spaces [3, pp. 198-201], [4].

The symbol S(X) denotes the semigroup, under composition, of all continuous selfmaps of the topological space X. This paper really grew out of our efforts to determine all those congruences σ on S(X) such that S(X)/σ is isomorphic to S(Y) for some space Y.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 38 , Issue 3 , 01 June 1986 , pp. 538 - 551
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Magill, K. D. Jr., Some homomorphism theorems for a class of semigroups, Proc. London Math. Soc. (3) 14 (1965), 517–526.Google Scholar
2. Magill, K. D. Jr., I-subsemigroups and α-monomorphisms, J. Austral. Math. Soc. (2) 76 (1973), 146–166.Google Scholar
3. Magill, K. D. Jr., A survey of semigroups of continuous selfmaps, Semigroup Forum 11 (1975/76), 189–282.Google Scholar
4. Warndoff, J. C., Topologies uniquely determined by their continuous selfmaps, Fund. Math. 66 (1969/70), 25–43.Google Scholar