Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T00:49:52.101Z Has data issue: false hasContentIssue false
  • English
  • Français

The Enumeration of Non-Isomorphic 2-Connected Planar Maps

Published online by Cambridge University Press:  20 November 2018

V. A. Liskovets  and
T. R. S. Walsh
V. A. Liskovets
Affiliation:
Minsk, USSR
T. R. S. Walsh
Affiliation:
University of Western Ontario, London, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Since Tutte initiated the systematic enumeration of planar maps [11], most of the literature on the subject has dealt with rooted maps (i.e., with maps whose automophism group has been trivialized by distinguishing a doubly-oriented edge). In particular, Tutte proved [11] that the number B′(n) of rooted planar 2-connected (i.e., non-separable) maps with n ≧ 1 edges is expressed by the formula

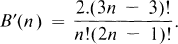
Recently one of the authors developed a general technique for enumerating unrooted planar maps considered up to orientationpreserving isomorphisms (see [6] and [8]). This technique, which is based on combinatorial map theory, Burnside’s lemma [3, p. 181] and the concept of a quotient map (see Section 1.4), was used to find, with little algebraic manipulation, simple counting formulae for the numbers of non-isomorphic planar maps of several types [7].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 35 , Issue 3 , 01 June 1983 , pp. 417 - 435
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. Babai, L., Imrich, W. and Lovasz, L., Finite homeomorphism groups of the 2-sphere, Colloq. Math. Soc. J. Bolya 8 (Topics in Topology, 1972), 61–75.Google Scholar
2. Coxeter, H. S. M., Introduction to geometry (J. Wiley, N. Y., 1961).Google Scholar
3. Harary, F., Graph theory (Addison Wesley, Reading, Mass., 1969).CrossRefGoogle Scholar
4. Jacques, A., Constellations et graphes topologiques, Colloq. Math. Soc. J. Bolyai 4 Combin. Th. and its Appl., vol. 2 (1969), 659–673.Google Scholar
5. Jones, G. A. and Singerman, D., Theory of maps on orientable surfaces, Proc. London Math. Soc. 37 (1978), 273–307.Google Scholar
6. Liskovets, V. A., A census of non-isomorphic planar maps, Colloq. Math. Soc. J. Bolyai 25, Algebraic Methods in Graph Th. 1978, (1981), 479–494.Google Scholar
7. Liskovets, V. A., Enumeration of non-isomorphic planar maps, J. Graph Theory 5 (1981), 115–117.Google Scholar
8. Liskovets, V. A., Enumerating non-isomorphic planar maps I (Russian), Questions of group theory and homological algebra, Jaroslavl (1981), 103–115, and Liskovets, V. A., Enumerating non-isomorphic planar maps II (Russian), Geometric methods in problems of analysis and algebra, Jaroslavl (1981), 106–117.Google Scholar
9. Mani, P., Automorphismen von polyhedrischen Graphen, Math. Ann. 192 (1971), 279–303.Google Scholar
10. Massey, W. S., Algebraic topology, an introduction (Harcourt, Brace & World, N. Y., 1967).Google Scholar
11. Tutte, W. T., A census of planar maps, Can. J. Math. 75 (1963), 249–271.Google Scholar
12. Walsh, T. R., Generating non-isomorphic maps without storing them, SIAM Journal on Discrete and Algebraic Methods 4 (1983), 161–178.Google Scholar
13. Walsh, T. R., Counting non-isomorphic three-connected planar maps, J. Combin. Th. 32B (1982), 33–44.Google Scholar
14. Whittaker, E. T. and Watson, G. N., A course in modern analysis (Cambridge Univ. Press. Cambridge, 1940).Google Scholar
15. Wormald, N. C., Counting unrooted planer maps, Discrete Mathematics 36 (1981), 205–225.Google Scholar