Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T01:05:36.486Z Has data issue: false hasContentIssue false
  • English
  • Français

End Behaviour and Ergodicity for Homeomorphisms of Manifolds with Finitely Many Ends

Published online by Cambridge University Press:  20 November 2018

S. Alpern  and
V. Prasad
S. Alpern
Affiliation:
London School of Economics, London, England
V. Prasad
Affiliation:
York University, North York, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The recent paper of Berlanga and Epstein [5] demonstrated the significant role played by the “ends” of a noncompact manifold M in answering questions relating homeomorphisms of M to measures on M. In this paper we show that an analysis of the end behaviour of measure preserving homeomorphisms of a manifold also leads to an understanding of some of their ergodic properties, and allows results previously obtained for compact manifolds to be extended (with qualifications) to the noncompact case. We will show that ergodicity is typical (dense Gδ) with respect to various compact-open topology closed subsets of the space 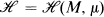consisting of all homeomorphisms of a manifold M which preserve a measure μ. It may be interesting for topologists to note that we prove when M is a σ-compact connected n-manifold, n≧ 2, then M is the countable union of an increasing family of compact connected manifolds. If M is a PL or smooth manifold, this is well known and easy. If M is just, however, a topological n-manifold then we apply the recent results [9] and [12] to prove the result. The Borel measure μ, is taken to be nonatomic, locally finite, positive on open sets, and zero for the manifold boundary of M.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 39 , Issue 2 , 01 April 1987 , pp. 473 - 491
Copyright
Copyright © Canadian Mathematical Society 1987

References

1. Alpern, S., Approximation to and by measure preserving homeomorphisms, J. London Math. Soc. 18 (1978), 305–315.Google Scholar
2. Alpern, S., Generic properties of measure preserving homeomorphisms, Ergodic Theory, Proceedings Oberwolfach (1978), Springer Lecture Notes in Math. 729 (1979), 16–27.Google Scholar
3. Alpern, S., Return times and conjugates of an antiperiodic transformation, Erg. Th. and Dyn. Sys. 1 (1981), 135–143.Google Scholar
4. Alpern, S., Nonstable ergodic homeomorphisms of R 4 , Indiana U. Math. J. 32 (1983), 187–191.Google Scholar
5. Berlanga, R. and Epstein, D., Measures on sigma compact manifolds and their equivalences under homeomorphisms, J. London Math. Soc. 27 (1983), 63–74.Google Scholar
6. Choksi, J. and Kakutani, S., Residuality of ergoclic measurable transformations and of ergodic transformations which preserve an infinite measure, Indiana U. Math. J. 28 (1979), 453–459.Google Scholar
7. Fathi, A., The structure of homeomorphisms preserving a good measure, Ann. Scient. Ec. Norm. Sup. 13 (1980), 45–93.Google Scholar
8. Katok, A. and Stepin, A., Metric properties of measure preserving homeomorphisms, Uspekhi Math. Nauk 25 (1970), 193–222, translated in Russian Math. Surveys 25 (1970), 191–220.Google Scholar
9. Kirby, R. and Siebenmann, L., Foundational essays on topological manifolds, smoothings and triangulations, Annals of Math. Studies 88 (Princeton Univ. Press, 1977).CrossRefGoogle Scholar
10. Oxtoby, J. and Ulam, S., Measure preserving homeomorphisms and metrical transitivity, Ann. of Math. 42 (1941), 874–920.Google Scholar
11. Prasad, V. S., Ergodic measure preserving homeomorphisms of R n , Indiana U. Math. J. 28 (1979), 859–867.Google Scholar
12. Quinn, F., Ends of maps III, J. Diff. Geom. 17 (1982), 503–521.Google Scholar
13. Schwartzman, S., Assymptotic cycles, Ann. of Math. 66 (1957), 270–284.Google Scholar
14. Thurston, W., On the structure of the group of volume preserving diffeomorphisms, preprint.Google Scholar