Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Trotter, P. G.
1972.
A class of semigroups embeddable in groups.
Semigroup Forum,
Vol. 5,
Issue. 1,
p.
1.
Tamari, Dov
1973.
Word Problems - Decision Problems and the Burnside Problem in Group Theory.
Vol. 71,
Issue. ,
p.
591.
Bouleau, N
1973.
Conditions unilatérales d'immersibilité d'un semi-groupe dans un groupe et un contre-exemple à un résultat de A. H. Clifford et G. B. Preston.
Journal of Algebra,
Vol. 24,
Issue. 2,
p.
197.
Faith, Carl
1976.
Algebra II Ring Theory.
Vol. 191,
Issue. ,
p.
109.
Osondu, Kevin E.
1984.
Malcev sequences and associative symmetrisations.
Semigroup Forum,
Vol. 29,
Issue. 1,
p.
61.
JOHNSTONE, P. T.
2008.
On embedding categories in groupoids.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 145,
Issue. 2,
p.
273.
Hollings, Christopher
2009.
The Early Development of the Algebraic Theory of Semigroups.
Archive for History of Exact Sciences,
Vol. 63,
Issue. 5,
p.
497.
Hollings, Christopher
2014.
Embedding semigroups in groups: not as simple as it might seem.
Archive for History of Exact Sciences,
Vol. 68,
Issue. 5,
p.
641.
Garrão, A. P.
Martins-Ferreira, N.
Raposo, M.
and
Sobral, M.
2020.
Cancellative conjugation semigroups and monoids.
Semigroup Forum,
Vol. 100,
Issue. 3,
p.
806.
Edwardes, Milo
and
Heath, Daniel
2025.
A collection of cancellative, singly aligned, non-group embeddable monoids.
Semigroup Forum,
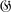 is said to be embeddable in a group if there exists a group
is said to be embeddable in a group if there exists a group 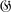 which contains a subsemigroup isomorphic to
which contains a subsemigroup isomorphic to 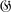 .
.