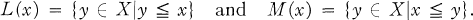Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T00:37:50.240Z Has data issue: false hasContentIssue false
  • English
  • Français

Embedding Smooth Dendroids in Hyperspaces

Published online by Cambridge University Press:  20 November 2018

J. Grispolakis  and
E. D. Tymchatyn
J. Grispolakis
Affiliation:
University of Saskatchewan, Saskatoon, Saskatchewan
E. D. Tymchatyn
Affiliation:
University of Saskatchewan, Saskatoon, Saskatchewan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A continuum will be a connected, compact, metric space. By a mapping we mean a continuous function. By a partially ordered space X we mean a continuum X together with a partial order which is closed when regarded as a subset of X × X. We let 2x (resp. C(X)) denote the hyperspace of closed subsets (resp. subcontinua) of X with the Vietoris topology which coincides with the topology induced by the Hausdorff metric. The hyperspaces 2X and C(X) are arcwise connected metric continua (see [3, Theorem 2.7]). If A ⊂ X we let C(A) denote the subspace of subcontinua of X which lie in A.

If X is a partially ordered space we define two functions L, M : X → 2X by setting for each x ∊ X

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 31 , Issue 1 , 01 February 1979 , pp. 130 - 138
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Carruth, J. H., A note on partially ordered compacta, Pacific J. Math. 24 (1968), 229–231.Google Scholar
2. Fugate, J. B., Small retractions of smooth dendroids onto trees, Fund. Math. 71 (1971), 255–262.Google Scholar
3. Kelly, J. L., Hyperspaces of a continuum, Trans. Amer. Math. Soc. 52 (1942), 22–36.Google Scholar
4. Krasinkiewicz, J., On the hyperspaces of hereditarily indecomposable continua, Fund. Math. 84 (1974), 175–186.Google Scholar
5. Nadler, S. B., Jr. Hyperspaces of Sets, to appear, (Marcel Dekker, Inc., New York).Google Scholar
6. Tymchatyn, E. D., Antichains and products in partially ordered spaces, Trans. Amer. Math. Soc. 146 (1969), 511–520.Google Scholar
7. Transue, W. R. R., On the hyperspace of subcontinua of the pseudo-arc, Proc. Amer. Math. Soc. 18 (1967), 1074–1075.Google Scholar
8. Whitney, H., Regular families of curves, Annals of Math. 34 (1933), 244–270.Google Scholar