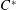Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-24T01:29:45.740Z Has data issue: false hasContentIssue false
  • English
  • Français

Elements of $C^{\ast }$-algebras Attaining their Norm in a Finite-dimensional Representation

Part of: Selfadjoint operator algebras General theory of linear operators

Published online by Cambridge University Press:  09 January 2019

Kristin Courtney  and
Tatiana Shulman
Kristin Courtney
Affiliation:
University of Virginia, Charlottesville, VA 22904, United States Email: [email protected]
Tatiana Shulman
Affiliation:
Department of Mathematical Physics and Differential Geometry, Institute of Mathematics of Polish Academy of Sciences, Warsaw Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We characterize the class of RFD 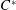$C^{\ast }$-algebras as those containing a dense subset of elements that attain their norm under a finite-dimensional representation. We show further that this subset is the whole space precisely when every irreducible representation of the 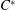$C^{\ast }$-algebra is finite-dimensional, which is equivalent to the 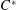$C^{\ast }$-algebra having no simple infinite-dimensional AF subquotient. We apply techniques from this proof to show the existence of elements in more general classes of 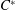$C^{\ast }$-algebras whose norms in finite-dimensional representations fit certain prescribed properties.

Keywords

AF-telescopesRFDprojective

MSC classification

Primary: 46L05: General theory of $C^*$-algebras
Secondary: 47A67: Representation theory
Type
Article
Information
Canadian Journal of Mathematics , Volume 71 , Issue 1 , February 2019 , pp. 93 - 111
Copyright
© Canadian Mathematical Society 2017 

Footnotes

The research of author T. S. was supported by the Polish National Science Centre grant under the contract number DEC-2012/06/A/ST1/00256 and by the Eric Nordgren Research Fellowship Fund at the University of New Hampshire.

References

Akemann, C. A. and Pedersen, G. K., Ideal perturbation of elements in C ∗-algebras . Math. Scand. 41(1977), 117–139. https://doi.org/10.7146/math.scand.a-11707.Google Scholar
Archbold, R. J., On residually finite-dimensional C ∗-algebras . Proc. Amer. Math. Soc. 123(1995), no. 9, 2935–2937. https://doi.org/10.2307/2160599.Google Scholar
Bekka, B., Operator superrigidity for SL n (ℤ), n⩾3 . Invent. Math. 169(2007), no. 2, 401–425. https://doi.org/10.1007/s00222-007-0050-5.Google Scholar
Blackadar, B., Shape theory for C ∗-algebras . Math. Scand. 56(1985), 249–275. https://doi.org/10.7146/math.scand.a-12100.Google Scholar
Blackadar, B., Operator algebras. Theory of C ∗-algebras and von Neumann algebras. Operator Algebras and Non-commutative Geometry. III. Encyclopaedia of Mathematical Sciences, 122, Springer-Verlag, Berlin, 2006. https://doi.org/10.1007/3-540-28517-2.Google Scholar
Brown, N. P. and Ozawa, N., C ∗-algebras and finite-dimensional approximations. Graduate Studies in Mathematics, 88, American Mathematical Society, Providence, RI, 2008. https://doi.org/10.1090/gsm/088.Google Scholar
Choi, M. D., The full C ∗-algebra of the free group on two generators . Pacific J. Math. 87(1980), no. 1, 41–48. https://doi.org/10.2140/pjm.1980.87.41.Google Scholar
Davidson, K. R., C ∗-algebras by example. Fields Institute Monograph, 6, American Mathematical Society, 1996. https://doi.org/10.1090/fim/006.Google Scholar
Dixmier, J., C ∗-algebras. North-Holland Mathematical Library, 15, North Holland Publishing Co., Amsterdam-New York-Oxford, 1977.Google Scholar
Eilers, S. and Exel, R., Finite-dimensional representations of the soft torus . Proc. Amer. Math. Soc. 130(2002), no. 3, 727–731. https://doi.org/10.1090/S0002-9939-01-06150-0.Google Scholar
Exel, R. and Loring, T., Finite-dimensional representations of free product C ∗-algebras . Internat. J. Math. 3(1992), no. 4, 469–476. https://doi.org/10.1142/S0129167X92000217.Google Scholar
Fritz, T., Netzer, T., and Thom, A., Can you compute the operator norm? Proc. Amer. Math. Soc. 142(2014), 4265–4276. https://doi.org/10.1090/S0002-9939-2014-12170-8.Google Scholar
Glimm, J., Type I C ∗-algebras . Ann. of Math. 73(1961), 572–612. https://doi.org/10.2307/1970319.Google Scholar
Goodearl, K. R. and Menal, P., Free and residually finite-dimensional C ∗-algebras . J. Funct. Anal. 90(1990), 391–410. https://doi.org/10.1016/0022-1236(90)90089-4.Google Scholar
Grigorchuk, R., Musat, M., and Rørdam, M., Just-infinite C ∗-algebras. arxiv:1604.08774.Google Scholar
Hadwin, D., A lifting characterization of RFD C ∗-algebras . Math. Scand. 115(2014), no. 1, 85–95. https://doi.org/10.7146/math.scand.a-18004.Google Scholar
Hadwin, D. and Shulman, T., Stability of group relations under small Hilbert-Schmidt perturbations. arxiv:1706.08405.Google Scholar
Korchagin, A., Amalgamated free products of commutative C ∗-algebras are residually finite-dimensional . J. Operator Theory 71(2014), no. 2, 507–515. https://doi.org/10.7900/jot.2012jul03.1986.Google Scholar
Loring, T. A., Lifting solutions to perturbing problems in C ∗-algebras. Fields Institute Monographs, 8, American Mathematical Society, Providence, RI, 1997.Google Scholar
Loring, T. and Pedersen, G. K., Projectivity, transitivity, and AF-telescopes . Trans. Amer. Math. Soc. 350(1998), 4313–4339. https://doi.org/10.1090/S0002-9947-98-02353-8.Google Scholar
Loring, T. and Shulman, T., Lifting algebraic contractions in C ∗-algebras . Oper. Theory Adv. Appl. 233(2014), 85–92.Google Scholar
Lubotzky, A. and Shalom, Y., Finite representations in the unitary dual and Ramanujan groups. Discrete geometric analysis: proceedings of the first JAMS Symposium on Discrete Geometric Analysis (Sendai, Japan, 2002). Contemp. Math., 347, American Mathematical Society, Providence, RI, 2004, pp. 173–189. https://doi.org/10.1090/conm/347/06272.Google Scholar
Moore, C. C., Groups with finite-dimensional irreducible representations . Trans. Amer. Math. Soc. 166(1972), 401–410. https://doi.org/10.2307/1996058.Google Scholar
Sakai, S., C ∗-algebras and W ∗-algebras. Classics in Mathematics, Springer-Verlag, Berlin, 1971. https://doi.org/10.1007/978-3-642-61993-9.Google Scholar
Sakai, S., A characterisation of type I C ∗-algebras . Bull. Amer. Math. Soc. 72(1966), 508–512. https://doi.org/10.1090/S0002-9904-1966-11520-3.Google Scholar
Thom, A., Convergent sequences in discrete groups . Canad. Math. Bull. 56(2013), 424–433. https://doi.org/10.4153/CMB-2011-155-3.Google Scholar
Thoma, E., Über unitäre Darstellungen abzählbarer diskreter Gruppen . Math. Ann. 153(1964), 111–138. https://doi.org/10.1007/BF01361180.Google Scholar
Thoma, E., Ein Charakterisierung diskreter Gruppen vom Typ I . Invent. Math. 6(1968), 190–196. https://doi.org/10.1007/BF01404824.Google Scholar